Пожалуйста можете как-то по легче обесьнить предел последовательности и предел функций именно определение с эпсилон и т.д. я смотрел читал чото я гдето не догоняю и можете посоветовать книги по мат анализу,буду очень благодарен
Привет. Для начала, думаю стоит обсудить идею лимита последовательности.
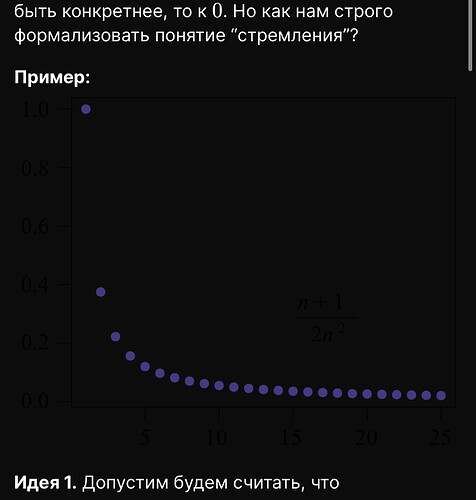
Посмотри на пример. Мы интуитивно чувствуем как последовательность с каждым последующим элементом “стремится” в какое-то значение, если быть конкретнее, то к 0. Но как нам строго формализовать понятие “стремления”?
Пример:
Идея 1. Допустим будем считать, что последовательность стремится к какому-то значению a если она становится всё ближе и ближе к a. Думаю это первая и самая интуитивная идея. НО, на самом деле наша последовательность становится ближе не только к 0, но и к другим значениям, например к -1 тоже. Тогда давай немного подумаем по другому.
Идея 2.
Давай теперь делать от обратного, нам дали значение a. Надо проверить, стремится ли последовательность к a или нет? Мы заметили, что если последовательность стремится к a, тогда она становится всё ближе и ближе к нашему значению. Тогда, давай будем расматривать область возле a, и какие члены последовательности лежат в ней. Назовём это \epsilon - окрестностью.
\epsilon - окрестность:
Идея вроде рабочая, но стоит заметить, не все элементы последовательности могут быть внутри нашей области. Несмотря на это с какого-то момента N_0, все наши точки лежат в окрестности.
Теперь нам остаётся только уменьшать \epsilon и смотреть находятся ли вся последовательность в нашей \epsilon - окрестности с какого-то момента N_0 или нет.
Используя кванторы, мы можем это записать как:
\forall \epsilon >0 \space(\exist N_0 \in \N \space ( \forall n \in \N \space(n \ge N_0 \implies |x_n -a| < \epsilon)))
Или по человечески: “для любого \epsilon > 0 существует такой N_0, что для любого n > N_0 выполняется |x_n -a| < \epsilon”.
Ура ![]() , это и есть \epsilon-\delta нотация для лимита последовательности.
, это и есть \epsilon-\delta нотация для лимита последовательности.
Надеюсь стало понятнее, лимит функции это обобщение лимита последовательности, думаю дальше там будет проще. Или можешь посмотреть интуитивное объяснение от 3Blue1Brown.
В качестве материалов, как всегда прекрасные материалы MIT OCW, например 18.100A с лекциями, сборниками задач и экзаменами. А, на русском ориентируясь на классику В.А. Зорич “Математический анализ” и лекции от Шапошникова в МГУ тык или тык
P.S. Я ещё не брал курс real analysis’а и никогда не имел преподавательского опыта. Поэтому объяснения могут содержать ошибки, а рекомендации сделаны субъективно и я вообще не имею право что-либо рекомендовать :D. Поэтому feel free to criticize.
P.S.
Все эти прекрасные картинки я взял с Wikipedia, где имеется не менее прекрасное разъеснения лимитов последовательностей. Большое спасибо авторам.
В порядке использования:
By Melikamp - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=24996344
By Ceranilo, CC BY-SA 4.0, File:Folgenglieder im KOSY.svg - Wikimedia Commons
By File:Epsilonschlauch.svg: CeraniloDerivative work: Stephan Kulla (User:Stephan Kulla) - Own work based on: Epsilonschlauch.svg, CC BY-SA 4.0, File:Epsilonschlauch2.svg - Wikimedia Commons
By Ceranilo, CC BY-SA 4.0, File:Epsilonschlauch.svg - Wikimedia Commons
By Ceranilo, CC BY-SA 4.0, File:Epsilonschlauch klein.svg - Wikimedia Commons
Очень красивое объяснение
у картинки просто фона нет. Включите светлую тему)
Всем огромное спасибо