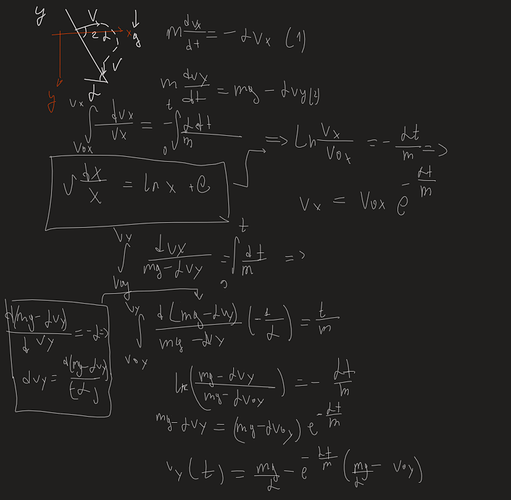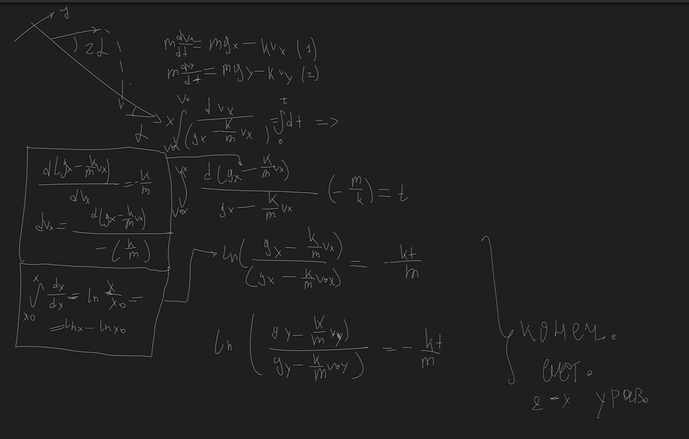Посогите решить, я написал дифференциальные уравнение
\frac{dv_x}{dt}=-\alpha V_x
\frac{dV_y}{dt}=-g-\alpha V_y
но суть в том что если поставить пределы и интегрирлвать то выйдет чушь, потому что V_x не может быть ноль, отсюда вопрос можно ли считать, что время в этом случае это время релаксации T=\frac{1}{\alpha} ?
Почему же не выходит?
В первом рисунке я показал твою “ошибку” - ты неправильно выбрал коорд. систему, в этой системе системе невозможно решить задачу
Во втором рисунке я привел правильное решение, то есть в котором я решал задачу в коорд. системе наклонной плоскости. Короче говоря, в конце у тебя выйдут два урав., выводы уже приведены. Думаю ты сам понимаешь и легко можешь сделать то, что здесь уже нужно все скорости и ускорения проецировать на выбранные оси.
почему в певых координатах решение неправильное, мы получили что
V_x=V_{0x} e^{-\alpha t} соотвестно нулю скорость может добраться через бесокнечно большое время
Скорее всего здесь неподходит выражение “неправильное”, я подразумевал то, что решение в первых координатах не принесет никакую пользу. Да конечно скорость на гориз. ось обнулится, значит экспонентой можно везде пренебречь, но так мы найдем только коэф. пропорциональности. Суть именно заключается в том, чтобы не искать те проекции скорости, которые обнулились - это не поможет в решении, а наоборот найти те проекции, которые можно вычислить и которые не равны нулю.
Это абсолютно верно, но парадокс в том, что таким образом ты лишаешься одного уравнения - на ось х и у тебя остается только одно уравнение, из которого нельзя найти время.
понятно спасибо