Извините за недоразумение, Ernur_Sabituly. Давайте попробуем вывести уравнение, указанное на второй картинке, шаг за шагом.
Вывод начинается с уравнения для химического потенциала растворителя A в растворе, который содержит нелетучее вещество B при температуре кипения ( T_b’ ) раствора:
[ \mu_A(l, x_{A1}, T_{b}‘) = \mu^*A(l, 1 atm, T{b}’) + RT \ln x_A ]
где:
- ( \mu_A(l, x_{A1}, T_{b}‘) ) - химический потенциал растворителя A в растворе при температуре кипения раствора ( T_b’ ).
- ( \mu^*A(l, 1 atm, T{b}‘) ) - химический потенциал чистого растворителя A при его температуре кипения ( T_b’ ) под давлением 1 атм.
- ( RT ) - произведение универсальной газовой постоянной и температуры кипения раствора.
- ( \ln x_A ) - натуральный логарифм мольной доли растворителя A.
Теперь, давайте рассмотрим фазовый переход между жидким и газообразным состоянием для растворителя A. В момент кипения раствора его химический потенциал в жидкой фазе равен химическому потенциалу в газообразной фазе:
[ \mu_A(l, x_{A1}, T_{b}‘) = \mu_A(g, 1 atm, T_{b}’) ]
Учитывая, что в момент кипения чистого растворителя A при его нормальной температуре кипения ( T_b^* ), его химический потенциал в жидкой фазе также равен его химическому потенциалу в газообразной фазе:
[ \mu^A(l, 1 atm, T{b}^) = \mu^A(g, 1 atm, T{b}^) ]
Так как добавление нелетучего вещества B приводит к повышению температуры кипения раствора до ( T_b’ ), мы можем записать:
[ \mu_A(g, 1 atm, T_{b}') = \mu^A(g, 1 atm, T{b}^) ]
Теперь мы можем выразить изменение температуры кипения ( \Delta T_b = T_b’ - T_b^* ) через изменение химического потенциала растворителя A в жидкой фазе, используя первое уравнение:
[ \mu^A(l, 1 atm, T{b}') + RT \ln x_A = \mu^A(g, 1 atm, T{b}^*) ]
После преобразования и выражения через ( \Delta T_b ), мы приходим к уравнению на второй картинке.
Этот процесс может требовать дополнительных упрощений и использования приближений, таких как уравнение Клапейрона-Клаузиуса, для связи изменения температуры кипения с мольной долей растворенного вещества. Если у вас есть доступ к полному тексту, откуда взяты эти уравнения, это может помочь уточнить и конкретизировать каждый шаг вывода.
Если вам нужны дополнительные пояснения или у вас есть конкретные вопросы по каждому шагу, пожалуйста, дайте знать.
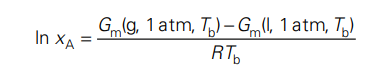
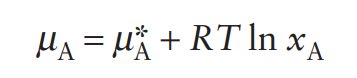
![]() под темой
под темой
