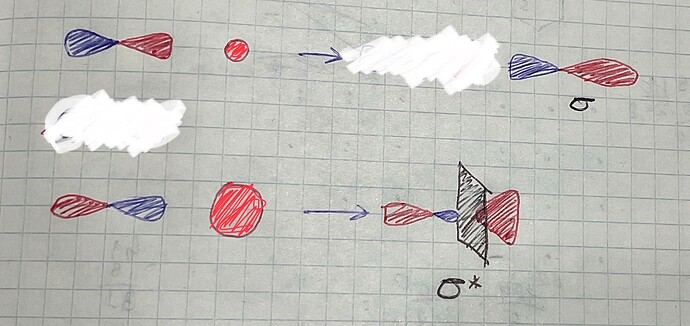
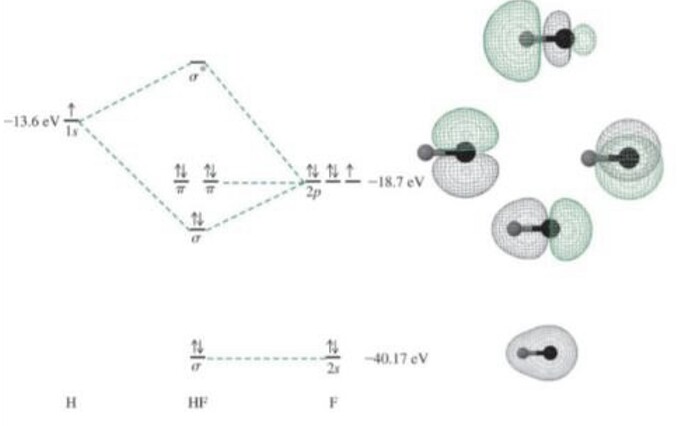
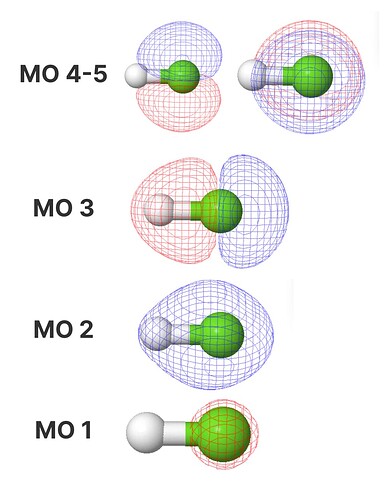
В общем, хз. Давайте сначала посмотрим какие орбитали получаются после расчетов:
С заполненными орбиталями никаких проблем нет - все как мы и ожидаем.
А вот со свободными орбиталями дело сложнее.
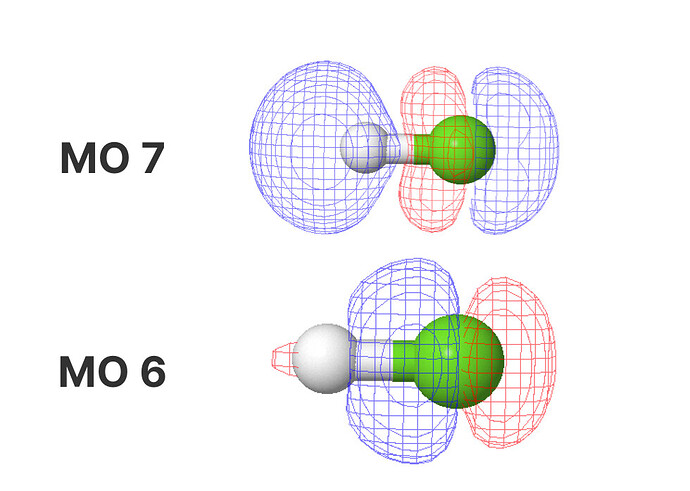
Я так полагаю все учебники в качестве LUMO берут MO7. Но, к слову, размер лопастей p орбитали фтора больше похож на то, что внутренняя и внешняя почти одинаковы, а может даже внешняя и чуть больше (как и предполагает наша интуиция).
Но при этом, MO 6 на \pu{11 эВ} ниже по энергии, чем MO 7. т.е. разница значительная. И здесь в принципе можно полностью запутаться.
Но важно понимать вот что - все квантовые расчеты это в какой-то мере взмах волшебной палочки, редко совпадающей с физическим смыслом. В каком плане: расчет сводится к тому, что мы берем определенный набор функций (условно АО) \phi_i, и нам надо найти коэффициенты c_i такие, чтобы функция \psi_i = \sum_i c_i \phi_i имела наименьшую энергию.
В какой-то степени это похоже на метод МО. Но вот если в методе МО мы берем 1s орбиталь водорода, 1s, 2s и 2p фтора (всего 6 АО), то в квантовых расчетах мы возьмем в 2-3 раза больше. Результаты выше получены с использованием 44 функций.
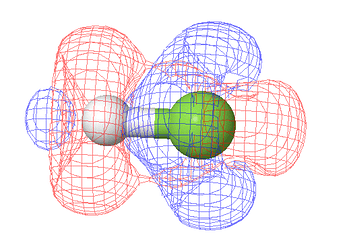
Например, MO 8 выглядит вот так:
Понятно что физического смысла у этого мало. Но использование 44 функций позволяет минимизировать суммарную энергию всех занятых орбиталей.
Иными словами, сам алгоритм Хартри Фока, в какой-то степени, придает гораздо больше физического смысла заполненным орбиталям, чем пустым (они даже и называются virtual). И в какой-то степени это логично, попробуйте сами ответить на вопрос: а что такое энергия свободной орбитали? Из чего она складывается?
Энергия свободной орбитали в Хартри-Фоке
Это энергия, которую имел бы электрон, если бы находился на этой орбитали. Т.е. она включает кулоновскую часть и exchange взаимодействие с электронами на всех заполненных орбиталях.
Короче, резюмируя:
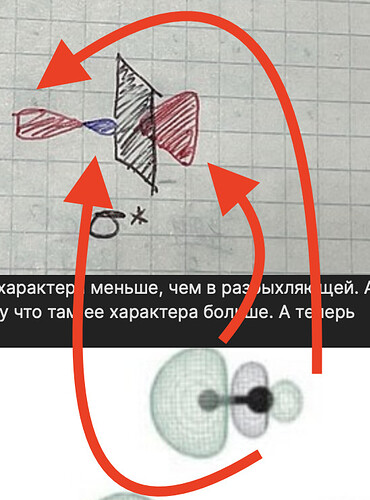
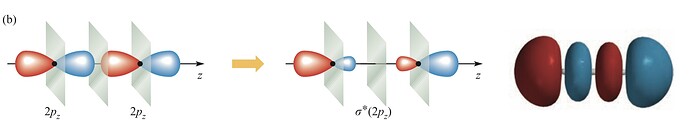
Аналитически (интуитивно). Действительно, ваша картинка \sigma^* больше соответствует общей интуиции о МО.
Фактически: мы не особо то знаем как на самом деле выглядит эта орбиталь (в микроскоп не увидишь). А картинки в учебниках основываются на результатах квантовых вычислений, которые имеют свои особенности.
Надеюсь вы поняли мою мысль.