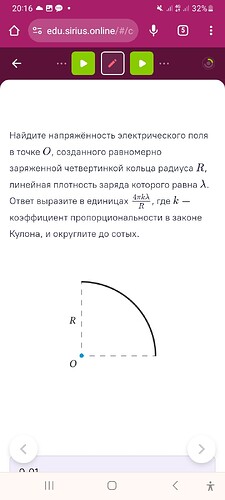
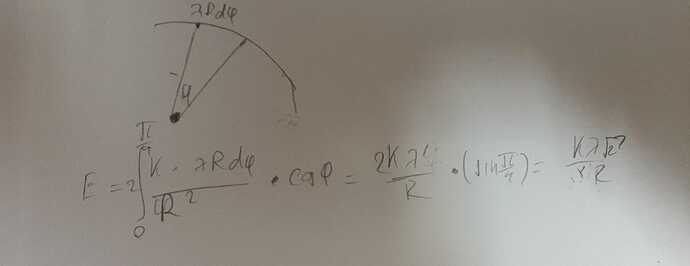Найдите напряжённость электрического поля в точке O�, созданного равномерно заряженной четвертинкой кольца радиуса R�, линейная плотность заряда которого равна λ�. Ответ выразите в единицах 4πkλ/R где k� — коэффициент пропорциональности в законе Кулона, и округлите до сотых.
У меня получился ответ k£/R и я не знаю как перевести в эту систему единиц, вроде получилась 1/4π но отве не сходиться
Киньте задачу скрином пожалуйста, и название сделайте поинформативней, и тему добавьте
скиньте решение пожалуйста, у меня другой ответ
Ну я посчитал что cosai×∆ri=это проекция на радиус
вообще кажется вы правильно делаете, но сумму нашли не правильно
у меня вот так
ещё вы кажется удвоить забыли, но хотя это смотря откуда до куда вы берёте пределы суммы, если как у меня то надо, если от -\frac{\pi}{4} до \frac{\pi}{4} то не надо удваивать
Не могли бы вы обесьнить как вы взяли подобный интеграл, тоесть как я понял мы при нахождений напряженности интегрируем по dl, как вы перешли к углам? Также не могли бы вы написать ваш конечный ответ, просто по рисунку я не смог разобрать (извините)
- интеграл табличный, мы знаем что d(\sin\varphi)=\cos\varphi \ d\varphi отсюда он выходит
- да по dl, но dl = R \ d\varphi, типа dl это длина дуги, а она равна центральный угол на радиус
- E = 2 \int_{0}^{\frac{\pi}{4}}\frac{k \lambda R \ d\varphi}{R^2} \cos\varphi=\frac{k \lambda \sqrt{2}}{R}
Ваш являеться правильным, спасибо за разесьнения, но я хотел бы уточнить почему мы берем предел π/4,вочему не π/2?
Типа я беру интерал от центра этой четверти до края, а там угол 45.
Понятно спасибо огромное