Объясните пожалуйста условие, а то я не пойму, например, почему точка двигается с постоянной скоростью, а нам надо найти ускорение. Я вижу, что там точка движется с постоянной скоростью по плоской траектории y(x), но, что это значит?
1 лайк
центростремительное ускорение
1 лайк
Можно какую-нибудь подсказку? А то я застрял на одном месте(dy/dt=2ax*dx/dt - вот, на что меня хватило)
ещё раз надо взять производную
2 лайка
Типо получится dy/dt = 2a?
Отсюда при x=0 получится
2a\cdot(\frac {dx}{dt})^{2} = 2av^{2}
3 лайка
Лучше так сформулирую, а почему у нас dx/dt = v?
да, потому что постоянная
1 лайк
Ок, спасибо
1 лайк
Добавлю ещё альтернативное решение, которое более сложное, но для него не нужно полагать x=0 для простоты.
Так как v=\text{const}, то в неподвижной системе отсчёта есть ускорение только центростремительное, т.е.
a=\frac{v^2}{R}.
И другой подход в решении заключается в том, чтобы определить зависимость радиуса кривизны R от формы траектории y(x).
Для этого нарисую произвольный график и выделю две близкие к нему точки
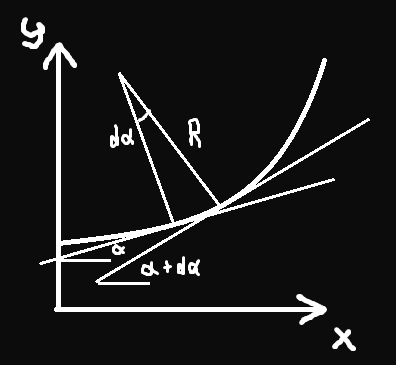
Для них касательные образуют углы \alpha и \alpha+d\alpha с осью x, а эти две точки объединены общей окружностью, точки которой разведены на угол d\alpha. Значит, с одной стороны, расстояние между двумя точками можно выразить как
Rd\alpha=\sqrt{dx^2+dy^2}=\sqrt{1+\dot y^2}\space dx,
где точки над y означают производную по x. С другой же стороны,
\tan \alpha = \dot y \quad \Rightarrow \quad \frac{d\alpha}{\cos^2\alpha} = \ddot y dx
Использую \displaystyle \frac{1}{\cos^2\alpha} = 1+\tan^2\alpha, тогда \displaystyle d\alpha = \frac{\ddot y}{1+\dot y^2} dx. Совмещаю с первым уравнением и получаю
R = \frac{(1+\dot y^2)^{3/2}}{\ddot y},
либо
a = \frac{v^2\cdot\ddot y}{(1+\dot y^2)^{3/2}}.
7 лайков
Сможете пж объяснить эту строчку?
первая точка находится в (x, y), вторая в (x+dx, y+dy), поэтому в линейном приближении расстояние между ними можно сложить «по пифагору»
1 лайк