Очень хорошее объяснение дал @amirbek. Я бы в целом сказал, что очень полезно вводить единичные вектора, если работаешь непосредственно с векторами. В объяснении выше подразумевается, что
\frac{d\vec\tau}{dt} = \omega\vec n=\frac{v}{R}\vec n.
Почему это так? Покажу на примере полярных координат:
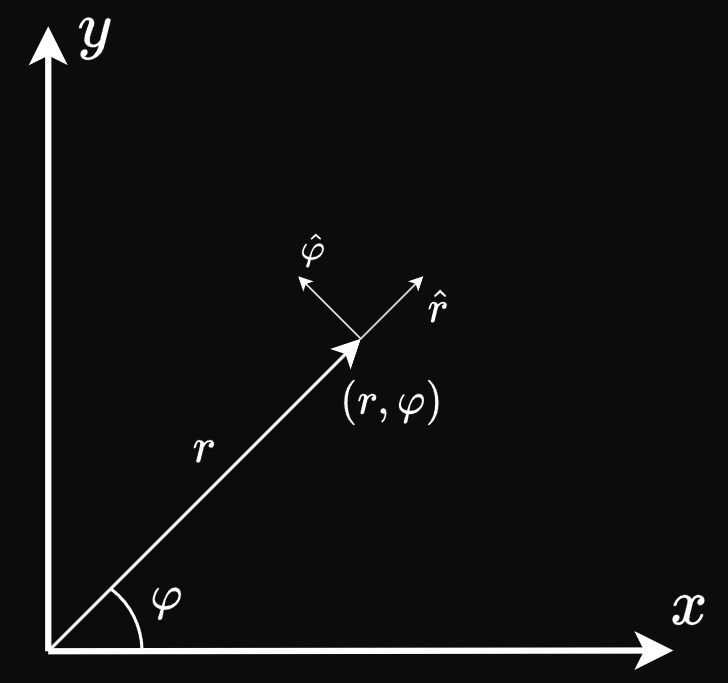
Здесь, в точке (r,\varphi) полярных координат, которая ставится в соответствие точке (x,y) декартовых, я расставил два единичных вектора. \hat r “пытается” увеличивать длину радиус-вектора (от начала координат к рассматриваемой точке); \hat\varphi же “пытается” увеличить угол \varphi от оси x к радиус-вектору.
Производная d/dt – это всегда скорость изменения некоторой величины по времени. Со скалярами всё понятно – их производная означает скорость изменения значения самого скаляра. Что же с векторами? Это означает как скорость изменения модуля вектора, так и скорость изменения его направления. Именно такую логику мы и наблюдаем, сделав:
Первое слагаемое означает скорость изменения значения |\vec v|, второе слагаемое – скорость поворота вектора \vec v. Теперь возвращаемся к моему случаю с полярными координатами.
Что, если взять производную от единичного вектора \hat r, например? Рассматривая её как функцию от времени t, то, по определению производной,
\frac{d\hat r}{dt} = \lim_{\Delta t\to0}\frac{\hat r(t+\Delta t)-\hat r(t)}{\Delta t}.
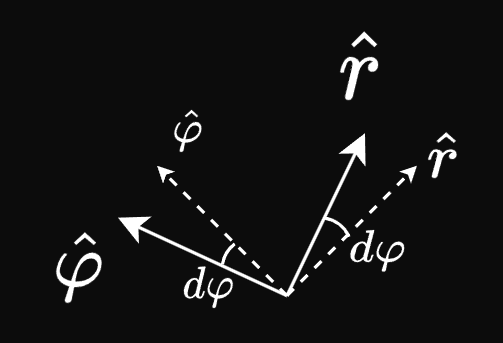
Геометрическое представление такого случая будет в таком виде:
Пара базисных векторов повернулась на небольшой угол d\varphi (в сторону приращения этого угла \varphi!) за небольшое время dt. Разность между “старым” и “новым” векторами \hat r представляется в виде очень маленького вектора \Delta\hat r, который соединяет концы этих двух \hat r. И если так приглядеться, то мы видим, что \Delta\hat r коллинеарен \hat\varphi. Значит справедливо сказать, что
\Delta\hat r = (1\cdot d\varphi)\hat\varphi.
Разделим это на dt – получим \displaystyle \dot{\hat r} = \dot{\varphi}\hat\varphi (точка сверху – другая форма записи d/dt). Такими же рассуждениями нетрудно понять, что \dot{\hat\varphi}=-\dot\varphi\hat r. Такое очень удобно применять на практике. Например:
\frac{d\vec r}{dt} = \frac{d}{dt}(r\hat r) = \dot r\hat r + r\dot{\hat r} = \dot r\hat r + r\dot\varphi\hat\varphi.
А ведь действительно – \dot r в первом слагаемом означает радиальную скорость, а r\dot\varphi – тангенциальную!
Можно в целом обобщить эту тему на производную произвольного вектора \vec A в виде разложения его на изменение модуля |\vec A| и его вращения с угловой скоростью \vec\omega. Тогда производная вектора может записываться в виде
\frac{d\vec A}{dt} = \frac{\delta\vec A}{\delta t} + \vec\omega\times\vec A.
В моём рассматриваемом случае здесь \vec A =\vec r=r\hat r, а \vec\omega = \dot\varphi\hat z. Тогда первое слагаемое есть \dot r\hat r (под \delta/\delta t я обозначил производную модуля вектора), а второе слагаемое есть \dot\varphi r(\hat z\times\hat r), где векторное произведение легко разрешается использованием детерминанта матрицы:
\hat z\times\hat r = \begin{vmatrix}\hat r&\hat \varphi&\hat z \\ 0&0&1 \\ 1&0&0\end{vmatrix} = \hat\varphi.
Тут вполне нормально использовать такой способ, поскольку (r,\varphi,z) является ортонормированным базисом – такие координаты лишь повёрнуты относительно (x,y,z) на угол \varphi, не более))
Итак, отвечая на вопрос темы: здесь \omega\equiv\dot\varphi, что полностью объясняет смысл производной вектора \vec\tau.