Чем отличается осестремительное ускорение от нормального? А также скажите пж, что такое ускорение Кориолиса?
2 лайка
Допустим тело движется так как показано тут:
Базис вектор (единичный вектор) в радиальном направлении:
\vec {\hat r}= \vec{\hat x}\cos \theta+\vec{\hat y}\sin \theta
Базис вектор (единичный вектор) в касательном направлении:
\vec {\hat \theta}= -\vec{\hat x}\sin \theta+\vec{\hat y}\cos \theta
Их производные:
{\vec{\hat{\dot r}}}=-\vec{\hat x}\dot \theta\sin\theta+\vec{\hat y}\dot \theta\cos \theta, \vec{\hat{\dot \theta}}=-\vec{\hat x}\dot \theta\cos \theta-\vec{\hat y}\dot \theta\sin\theta
Производные единичных векторов можно представить так:
{\vec{\hat{\dot r}}}=\dot \theta \vec{\hat \theta}, {\vec{\hat{\dot \theta}}}=-\dot \theta \vec {\hat r}
Радиус вектор можно представить так:
\vec r=\vec {\hat r}r
Возьмем ее производную:
\dot {\vec{r}}= {\vec{\hat{\dot r}}}r+{\vec{\hat r}}\dot r=\vec{\hat \theta}\dot\theta r+\vec{\hat r}\dot r
Вторую производную:
\ddot {\vec{r}}=\vec{\hat{\dot \theta}}\dot\theta r+\vec{\hat \theta}\ddot\theta r+\vec{\hat \theta}\dot\theta \dot r+\vec{\hat{\dot r}}\dot r+\vec{\hat r}\ddot r=-\vec{\hat r}\dot\theta^2 r+\vec{\hat \theta}\ddot\theta r+\vec{\hat \theta}\dot\theta \dot r+\vec {\hat \theta}\dot \theta \dot r+\vec{\hat r}\ddot r=\vec{\hat r}(\ddot r-\dot \theta^2 r)+\vec {\hat \theta}(2\dot \theta \dot r+\ddot \theta r)
Значит силу действующую на тело можно разбить на касательную и радиальную составляющую:
\vec F=m(\vec {\hat r}(\ddot r-\dot \theta^2 r)+\vec {\hat \theta}(2\dot \theta \dot r+\ddot \theta r))
Осестремительную силу можно выразить так:
\vec F_{cent}=-m\vec \omega\times(\vec \omega \times \vec r)
осестремительное ускорение направлено всегда от центра, и чтобы оно присутствовало тело не обязательно должно иметь скорость относительно вращающейся системы отсчета.
Силу кориолиса можно выразить так:
\vec F_{cor}=-2m\vec \omega \times \vec v
(upload://4Beh3QxpeNtFvUTblOwJQZTwzA0.png)
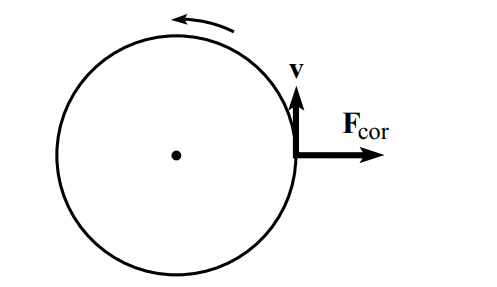
Чтобы на тело действовала сила Кориолиса оно должно иметь скорость относительно вращающейся системы отсчета. Ускорение кориолиса всегда направлено перпендикулярно вектору этой относительной скорости.
6 лайков
Рассмотрим движение по спирали постоянного радиуса (как пружинка) с какой-то скоростью (я не умею рисовать, так что воображение на максимум и вперёд)
Нормальное ускорение — ускорение, которое направлено под углом 90^\circ, оно меняет направление в зависимости от того, как направлена скорость
Осестремительное ускорение — ускорение которое направлено в центр. Плоскость xy перпендикулярна оси спирали
И a_o — ускорение которое обеспечивает проекцию в виде окружности для траектории
Ускорение Кориолиса
Сразу оговорюсь, что это тема республиканских сборов, и межнаров. Поэтому раньше времени её изучать не стоит, потому что перед ней нужно знать продвинутый математический аппарат: производные векторов, векторные произведения
Если совсем примитивно, то это ускорение, которое ввели для того, чтобы учитывать неинерциальность вращающихся систем отсчёта. Далее никаких сил трения нет. Если положить мячик в центр вращающегося диска и покатить его к краю, то относитильно стола, который неподвижен, траектория будет прямая, но относительно диска траектория будет искривлённой. Ускорение Кориолиса вводят чтобы “объяснить” это искривление в неинерциальной системе.
Если уж совсем интересно, то более подробно о нём можно почитать в Иродове параграф 1.3
6 лайков
ты, конечно, молодец, но учитывай уровень человека, который задаёт подобный вопрос) а ещё тебе это будет полезным: Как писать формулы? Язык разметки LaTeX
4 лайка
Честно говоря, я задал этот вопрос после прочтения данного параграфа)
1 лайк
Keep in mind that Coriolis acceleration is basically an illusion of acceleration.
It is the observer that is moving in a non-inertial frame of reference that views an object moving freely as having an acceleration
3 лайка