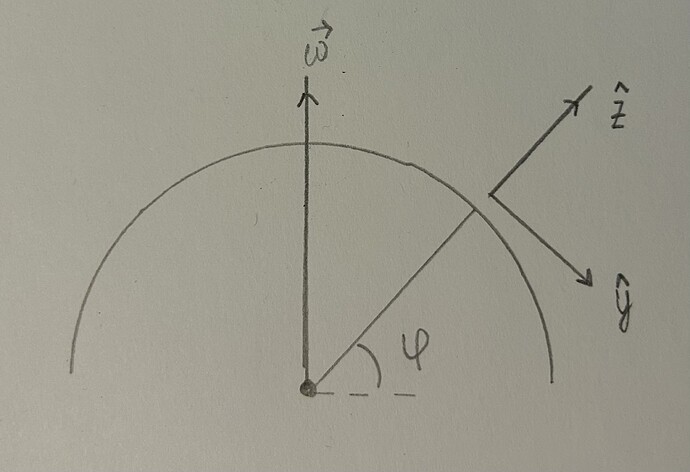\propto - знак пропорциональности.
Если че это выводится так:
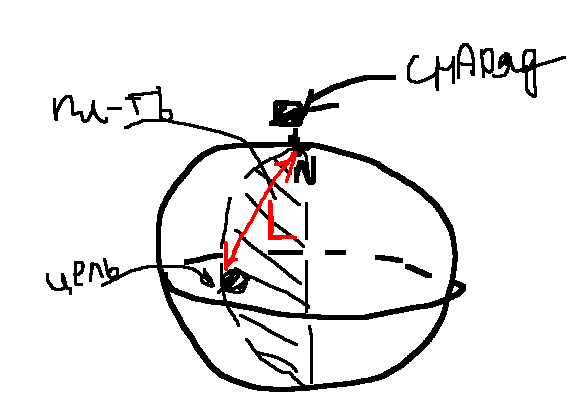
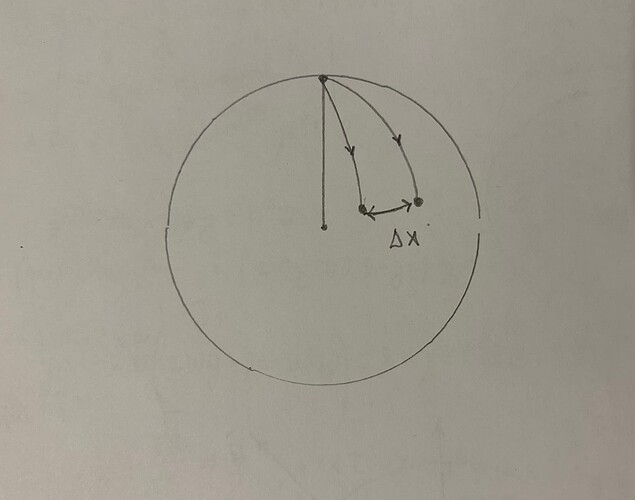
“Боковое смещение”, то есть смещение в экваториальной плоскости происходит за счет силы Кориолиса. Центробежной силой можно пренебречь, так как \vec\omega\times(\vec \omega \times \vec r)=\vec \omega(\vec \omega \cdot \vec r)-\omega^2\vec r\rightarrow \vec\omega\times(\vec \omega \times \vec r)\propto \omega^2\propto\frac{1}{T^2} она обратно пропорциональна квадрату периода вращения Земли вокруг своей оси и можно считать что время движения снаряда t<<T. Азимутальная сила \dot{\vec \omega}\times \vec r равна нулю, т.к. \vec \omega=const. Поэтому единственная сила инерции, которая оказывает влияния на снаряд это сила Кориолиса
\vec a=\vec a'+2\vec\omega\times \vec v'=-g\hat z
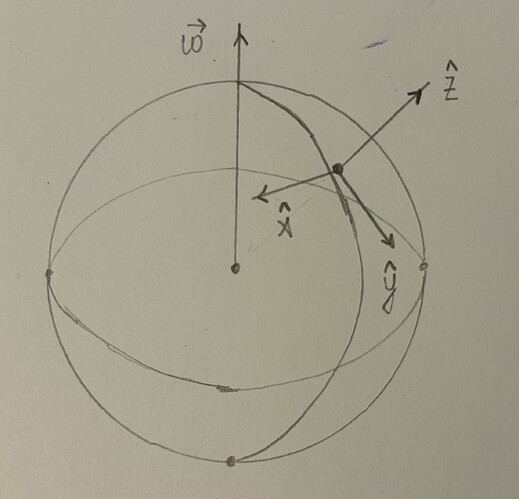
(Выбираю координатную систему так, что оси
x,y лежат на поверхности Земли, а ось
z направлена радиально)
Здесь
\vec a',\vec v' это ускорение и скорость во вращ. системе Земли и
\vec a'=\hat x\ddot x+\hat y\ddot y+\hat z\ddot z ,
\vec v'=\hat x\dot x+\hat y\dot y+\hat z\dot z. Разложим вектор угловой скорости вращения Земли вокруг своей оси по выбранному базису
\vec \omega=\begin{pmatrix}0\\-\omega\cos\varphi\\ \omega\sin\varphi \end{pmatrix}
Чтобы найти ускорение Кориолиса нужно выполнить векторное произведение
\vec a_{cor.}=-2\vec\omega\times\vec v'=-2\begin{vmatrix} \hat x& \hat y&\hat z\\0&-\omega\cos\varphi&\omega\sin\varphi\\ \dot x&\dot y&\dot z\end{vmatrix}=-2\omega(-\hat x(\dot z\cos\varphi+\dot y\sin\varphi)+\hat y(\dot x\sin \varphi)+\hat z(\dot x\cos\varphi))
Здесь скоростями \dot x,\dot y можно пренебречь по сравнению с \dot z, т.к. они сравнительно пренебрежимо малы \dot x,\dot y<<\dot z. Тогда уравнение движения
-g\hat z+2\omega \dot z\cos\varphi \hat x=\hat x\ddot x+\hat y\ddot y +\hat z\ddot z
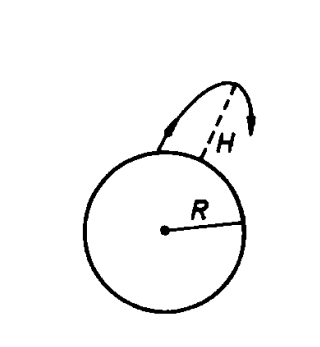
Отсюда получаем, что \ddot z=-g, следовательно \dot z=-gt\rightarrow z=h-\frac{gt^2}{2}, а также \ddot x =2\omega\dot z\cos\varphi=-2\omega gt\cos\varphi. Очевидно, что время падения снаряда t=\sqrt{\frac{2h}{g}}.; Модуль бокового смещения
\Delta x=\left(\frac{\omega gt^3}{3}\right)\cos\varphi=\left(\frac{\omega g}{3}\right)\left(\frac{2h}{g}\right)^{3/2}\cos\varphi
Из-за этого эффекта снаряд выпущенный на поверхности Земли не будет двигаться строго вдоль одной меридианы и отклонится на некое расстояние в экваториальной плоскости, за исключением случая, когда снаряд выпускается из северного полюса, для которого широта \varphi=\frac{\pi}{2}