В фантастическом рассказе описывается, как из-за небольшой оши-
бки в выборе начальной скорости при старте с поверхности Земли межпланетный
корабль падает на Солнце. При какой наименьшей скорости на поверхности Зем-
ли это возможно?
Минимальная скорость нужна, чтобы долететь кораблю до той точки, после которой он уже сам упадёт на Солнце.
Что это за точка?
Определи положение на отрезке между Солнцем и Землёй, при котором сила притяжения Земли равна силе притяжения Солнца. Через закон сохранения энергии нетрудно определить, собственно, и эту минимальную скорость.
Разве это будет минимальной скоростью?
Вспомним первый закон Кеплера:
Каждая планета солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце
Он применим не только планетам, но и всем другим телам, в частности, ракете из рассказа, после того, как она вышла из поля тяжести Земли. Тогда, нам нужно найти такую скорость, чтобы при движении ракеты по эллипсу, скорость в афелии (точке, наиболее удалённой от Солнца), была наибольшей
Почему скорость должна быть такой?
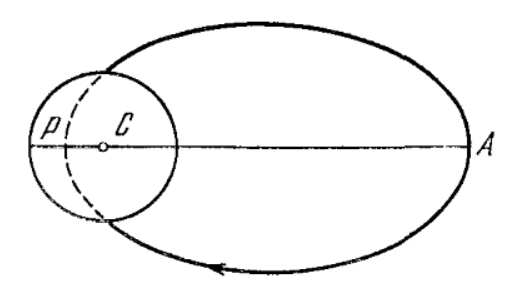
Для ответа на вопрос обратимся к схематичному изображению системы, где окружность – Солнце, эллипс – траектория объекта. Чем меньше его скорость, тем раньше он упадёт. Однако, ракета стартует с Земли, которая вращается по круговой орбите, то есть у неё уже есть скорость v_з. Когда ракета выходит из зоны притяжения Земли у неё скорость v_\infty, которую её можно найти через закон сохранения энергии. Эта скорость вычисляется в системе отсчёта Земли, поэтому для нахождения скорости в системе отсчёта Солнца, нужно учесть движение Земли по орбите. Для этого нужно векторно сложить скорость Земли и скорость ракеты, так чтобы энергия при получившейся скорости была наименьшей.
точно, забыл про орбитальную скорость Земли, спасибо