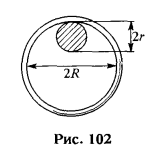
5.38. Определить период малых колебаний тонкого кольца массы M и радиуса R, надетого на неподвижный горизонтальный цилиндр радиуса r (рис. 102). Проскальзывания нет.
Я решил задачу с помощью мгновенной оси вращения:
mg \varphi R=I \varphi''
I=I_0+mR^2
I_0=mR^2
\omega=\displaystyle\sqrt{\frac{g}{2R}}
T=\displaystyle2 \pi \cdot \sqrt{\frac{2R}{g}}
В пруте ответ T=\displaystyle2 \pi R \cdot \sqrt{\frac{2}{g(R-r)}}
Где моя ошибка?
2 лайка
Во-первых, ось вращения кольца будет в центре горизонтального цилиндра. И попробуй эту задачу решить энергией – так гораздо проще будет.
1 лайк
Тогда получается так:
I=mR^2 +m(R-r)^2
(I(φ’)^2)/2 + mg(R-r)(1-cosφ)=E
(I(φ’)^2)/2 + mg(R-r)(1-(1-(φ^2)/2)=E
Беря производную по времени:
Ιφ’φ’‘+mgRφφ’=0
w=sqrt[g(R-r)/(R^2+(R-r)^2) ]
Если пренебречь r в нижней части то выйдет правильный ответ, но в задаче не сказано что R>>r
1 лайк
В этой задаче скорее всего так и нужно предполагать, что R>>r, т.к. иначе ответ в учебнике не выйдет, хотя решено у тебя все правильно
1 лайк
Вообще, я думаю, что можно и без этого предположения. Кольцо своей внутренней поверхностью “едет” по внешней поверхности цилиндра, и ввиду отсутствия проскальзывания относительная скорость между соприкасающимися поверхностями равна нулю.
Поэтому, видимо, я был неправ, а мгновенная ось вращения и вправду находится на поверхности кольца – хоть это и выглядит контринтуитивно, так как кольцо как фигура вращается относительно центра цилиндра, – в таком случае момент инерции реально J=mR^2+mR^2. То есть выйдет уравнение
E=2mR^2\cdot\frac{\dot\varphi^2}{2}+mg(R-r)(1-\cos\varphi),
из которого дифференцированием мы и получим нужный ответ.
Для визуализации я быстренько накидал анимацию в десмосе (которая работает если проматывать параметр a). По идее, если бы мгновенная ось вращения действительно находилась бы в центре цилиндра, то она, в силу симметрии системы, была бы неподвижна в пространстве, а значит все элементы кольца якобы должны постоянно вращаться вокруг точки, которая не находится в геометрическом их центре. Противоречие.
А так, интересно было бы послушать другие способы решения этой задачи. Она приходила на декабрьских сборах 2022 года, и правильный ответ у нас получило вроде только два человека, которые и то запомнили этот ответ из Прута задолго до контрольных))
9 лайков