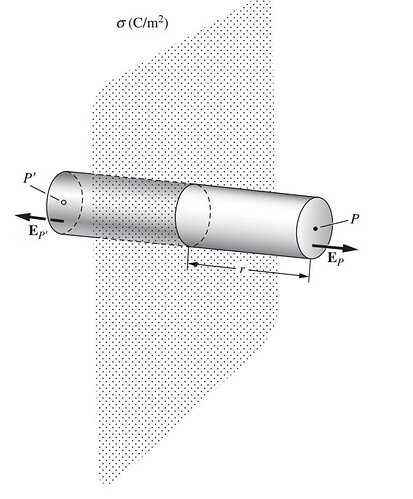
Найти максимальное электрические поля в зависимости от расстояние от центра симметрии двух нитей
3 лайка
Как взять dq?
Нужно ли использовать формулу E=σ/2ε0?
dΕ=κdq/x²
dq=ρdV
dV=к чему?
Можно, но не в этой задаче. Данную формулу находят с использование теоремы Гаусса, зная это можно также найти похожую формулу, но с использованием \lambda. Думаю ты такое уже делал, но заранее скажу, что можно вывести это уравнение, делая нить в виде цилиндра.
3 лайка
Очевидно для заряженной нити это:
dq=\lambda dl
где \lambda это линейная плотность заряда на нити
Ну если ты задаешь такой вопрос то значит тебе все это нужно хорошенько объяснить:
по теореме гаусса для плоскости с площадью S и по обеим сторонам которого есть одинаковые и противоположно направленные вектора напряженностей. Тогда естественно поток запишется так:
Ф=\int_S \vec E \vec {dS}=E(2S)=\frac{\sigma S}{\varepsilon_0}
Но у тебя в задаче равномерно заряженные нити, поэтому теорему гаусса выглядит таким образом (площадью через которую ты рассматриваешь поток вектора напряженности будет цилиндром с радиусом равным перпендикулярному расстоянию от нити):
Ф=\int_S \vec E \vec {dS}=E(2\pi rl)=\frac{\lambda l}{\varepsilon_0}
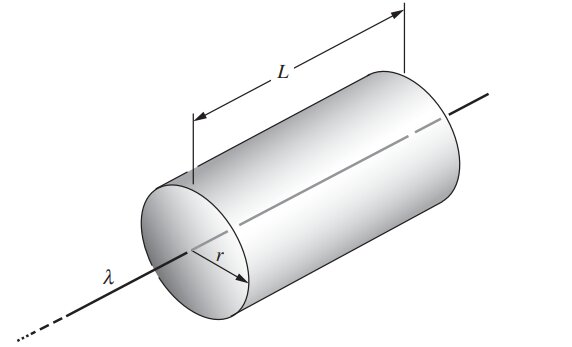
Это верно и тут x должен выступать как расстояние от нити r
Нить предполгается супер тонкой и одномерной, поэтому dq берешь так, как было показано выше
Ну подумай сам, допустим у тебя есть тонкая сфера, толщину можно даже взять как ноль, тогда заряды по этой сфере можно распределить только по ее поверхности (это же справедливо и для полого цилиндра):
dq=\sigma dS
А теперь допустим есть шар, он занимает какой то объем в пространстве, значит заряды по шару можно распределить по ее объему: (так же и для не полого цилиндра)
dq=\rho dV
А тонкая нить это штука одномерная, у нее есть только длина, тогда заряды по нити можно распределить только по ее длине:
dq=\lambda dl
6 лайков