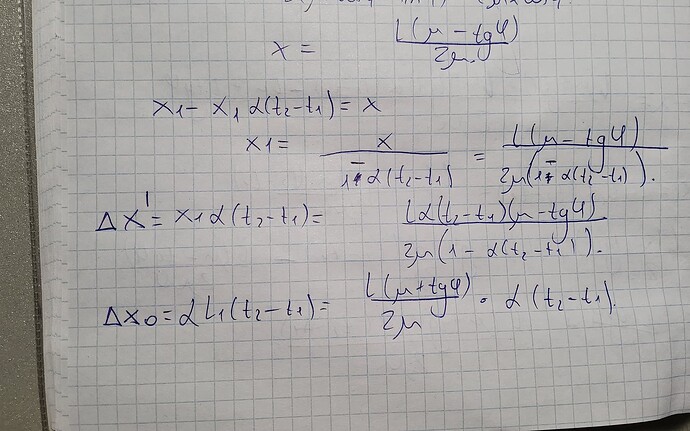Ну смотри при нагревании неподвижные точки располагаются в одном месте, в при охлаждений в другом, соответственно расстояния между нижней частью и неподвижными точками другие. Думаю не будет вопросов по этому утверждению, так как в самом заданий просят положение неподвижных точек при нагревании и охлаждении)
Чтоооооо,я это и не учитывал,ну я прочто про это не знал короче)
Если брать что изначально расстояние между нижней частью и новой неподвижной линией было x1 то у нас опять что-то не выходит)
Вы пытаетесь рассмотреть второй цикл нагревания и охлаждения?) Если уж такое дело новое расположение неподвижной точки скажем уже при нагревании, будет на \Delta S раз ближе в нижнему концу.
Нет)Я тут нахожу насколько вверх поднялся нижний конец и результат не сходится с решением.Посмотрите как я вывожу dx’
Если рассматривать все с точки зрения динамики,
mg\sin{\phi}-\mu mg\frac{l-x_1}{l}\cos{\phi} +\mu mg\frac{x_1}{l}\cos{\phi}=0\Rightarrow\\
l\sin{\phi}-\mu l\cos{\phi}+\mu x_1\cos{\phi} +\mu x_1\cos{\phi}=0\Rightarrow\\
x_1=l\frac{\sin{\phi}-\mu \cos{\phi}}{2\mu \cos{\phi}}\Rightarrow\\
\Delta x_1=\frac{\alpha L(t_1-t_2)}{2\mu }\frac{\sin{\phi}-\mu \cos{\phi}}{2\mu \cos{\phi}}
все соответствует и все логично 
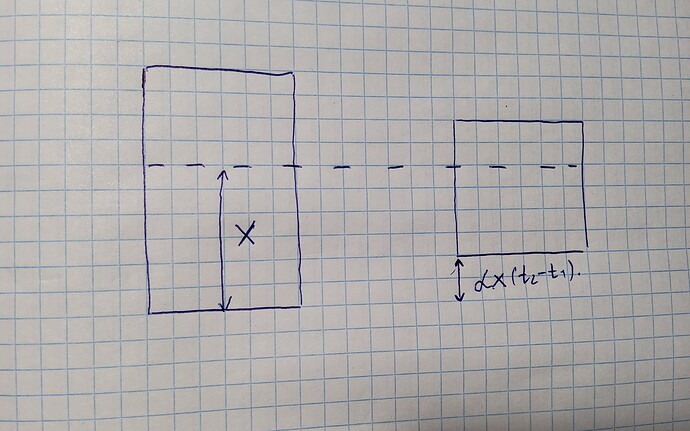
Охлаждение, верно? Можно подробнее, что такое x?
1 лайк
1)вы когда x1 выводили в конце перепутали местами в числителе значения(у вас отрицательно типо вышло)
2)Мое x=ваше x1
верно
Во первых, у меня ничего не перепутана. У меня местами поменялись не один, а два локальных уравнения внутри одной формулы. Соответственно разность температур и разность углов, и если из них вывести по (-1), то ничего не изменится, будет так же как и в решении.
Тогда тут ошибка в том, что мой x_1- это начальная длина до охлаждения, а значит я могу пользоваться формулой линейного расширения. А ваш x_1 представляет собой конечную длину листа после охлаждения, а значит соответственно мы не можем пользоваться линейным расширением для конечной длины листа.
А как это может быть начальная длина до охлаждения,если вы уже использовали факт того что у вас пластинка длиной L когда выводили x1
У нас же нагрев,пластина удлинилась,а потом охлаждение и пластина возвращает начальную форму
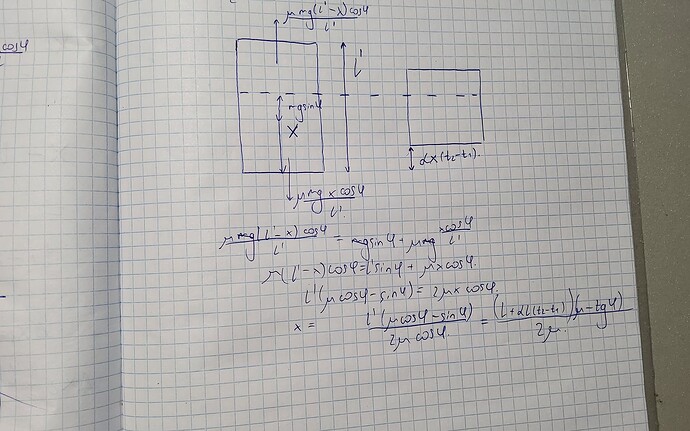
Я использовал тот факт, что длина всей пластинки равна l при температуре t_2 и до охлаждения расположение неподвижных точек было на расстоянии x_1. А сжатие будет принимать то же поведение с охлаждение всего.
Так это не противоречит тому, что я написал. Ведь я взял начальную длину как L, а ее переменную как l.
Мы уже тут на долгое время засиделись и я советую решить другие задачи, затем со свежей головой снова прочитать решение этой задачи.
3 лайка
Под конец дня хотел сказать что при температуре t2 у пластины расстояние уже не l ,у нас же расширилась пластина
Прошу это снова прочитать) Вот поэтому, нужно иногда посидеть и попить горячего, подрящего чая с плюшками, чтобы не путаться потом.
1 лайк
А.с. ещё раз)Я правильно понял ваш вчерашний ход решений?
Если нет можете пожалуйста рисунок нарисовать,а то я так до завтра буду мне кажется)
Да, только перепутал температуры, но в зависимости от направления смещения можно и так)
Вот этот момент я у вас хотел спросить,почему типо мы берём L(начальная длина пластины) ,у меня просто L’(удлиненная пластинка)
Сори что уже 2 день вас с этой задачей тревожу,просто мне ее надо по скорее решить
Смотри по вашему рисунку видно, что начальная длина всего до охлаждения некая l', потом в процессе очень долгого охлаждения лист будет сужаться в зависимости от температуры. Мы берем l' как начальную длину, так как расположение неподвижных точек в разных процессах находится в разных местах. Сила трения играет роль только некой “опоры” для листа, чтобы он не скатился с крыши, а в ином случае лист будет просто падать. Так что, тут нужно смотреть только относительно линейного расширения листа, а сам механизм линейного расширения основано на изменений начальных размеров какого либо тела в зависимости от его температуры.
Вы же нашли решение в интернете и оно решено верно.
3 лайка