7.7. Rutherford scattering ***
A particle of mass m travels in a hyperbolic orbit past a mass M, whose
position is assumed to be fixed. The speed at infinity is v0, and the impact
parameter is b (see Exercise 7.14).
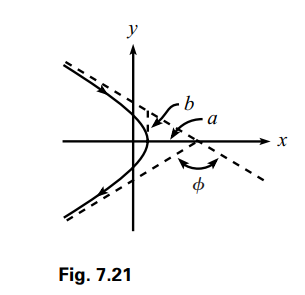
(a) Show that the angle through which the particle is deflected is
\phi=\pi-2tan^-1(\gamma b) => b=\frac{1}{\gamma}\cot(\frac{\phi}{2})
(b) Let dσ be the cross-sectional area (measured when the particle
is initially at infinity) that gets deflected into a solid angle of size
d\Omega at angle φ. Show that
\frac{d\sigma}{d\Omega}=\frac{1}{4\gamma^2 \sin^2(\frac{\phi}{2})}
С пунктом (а) я справился, в пункте (б) я не очень понимаю условие, а соответственно решение тоже. Конкретно не понимаю как это выглядит, нарисуйте чертёж на котором все эти углы показаны, пожалуйста