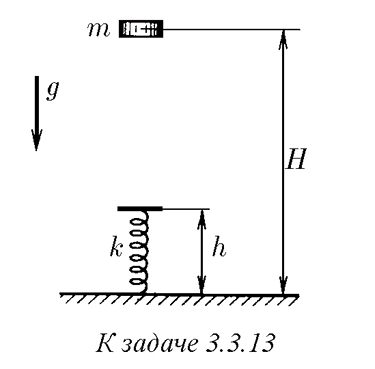
3.3.13.Груз массы m падает с высоты H на пружину жесткости k и длины h, нижний конец которой прикреплен к полу. Определите время контакта груза с пружиной, если mg < 2k(H −h).
можете помочь с записью уравнения колебаний.
Здесь скорость в момент столкновения с пружиной равен \sqrt{2g(H-h)}, дальше уравнение движение груза m\ddot z=-kz+mg
да так и выходит но такое можно разве преобразовать в колебания или тут только интегралом можно решить?
У тебя же выходит такая диффура
\ddot z +\frac{kz}{m}-g=0\rightarrow \ddot z+\frac{k}{m}\left(z-\frac{mg}{k}\right)=0
Можешь сделать замену z-\frac{mg}{k}=\xi, тогда \ddot \xi+\frac{k\xi}{m}=0 и решение такого уравнения \xi(t)=z(t)-\frac{mg}{k}=A\cos\left(\sqrt{\frac{k}{m}}t+\varphi\right)
4 лайка
блин что то не подумал сделать замену, не встречалось до этого,спасибо за метод потом решу и галочку поставлю)