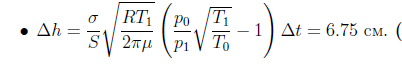Конечно, давайте подробно разберём задачу и объясним, как определить давления ( p_0 ) и ( p_1 ), а затем использовать их для нахождения изменения высоты поршня.
Исходные данные задачи:
- Масса поршня: ( M = 1 ) кг
- Площадь поршня: ( S = 10 ) см² ( = 10 \times 10^{-4} ) м²
- Общая площадь отверстий: ( \sigma = 0.01 ) см² ( = 0.01 \times 10^{-4} ) м²
- Температура внутри сосуда: ( T_1 = 400 ) К
- Температура окружающего воздуха: ( T_0 = 300 ) К
- Газовая постоянная: ( R = 8.31 ) Дж/(моль·К)
- Молярная масса воздуха: ( \mu = 29 ) г/моль ( = 0.029 ) кг/моль
- Время: ( t = 10 ) секунд
Понимание задачи:
Поршень отделяет сосуд от атмосферы. Когда Быстрый Ахмаджон проделывает отверстия, воздух начинает уходить через эти отверстия, что приводит к изменению давления внутри сосуда и, как следствие, к перемещению поршня.
Определение давлений ( p_0 ) и ( p_1 ):
-
( p_1 ) — давление внутри сосуда под поршнем.
-
( p_0 ) — атмосферное давление снаружи (на внешнюю сторону поршня).
Однако в условии задачи не приведено конкретное значение атмосферного давления. Но можно воспользоваться стандартным атмосферным давлением ( p_{атм} = 10^5 ) Па (если не указано иное).
Таким образом:
- ( p_0 = p_{атм} = 10^5 ) Па
- ( p_1 ) — давление внутри сосуда, которое будет меняться из-за выхода воздуха через отверстия.
Механика движения поршня:
Когда поршень находится в равновесии, силы равновесны:
[
p_1 S = p_0 S + Mg
]
Отсюда давление внутри сосуда:
[
p_1 = p_0 + \frac{Mg}{S}
]
Но с течением времени, когда воздух выходит, высота столба воздуха меняется, и ( p_1 ) будет зависеть от объёма воздуха, который покидает сосуд.
Моделирование выхода газа:
Поскольку отверстия маленькие, можно предположить, что процесс выхода газа является адиаабатическим (теплообмен не происходит из-за малой площади поверхности). Однако в условии сказано, что температура внутри сосуда поддерживается постоянной ( T_1 = 400 ) К. Это указывает на то, что процесс изотермический.
Для изотермического процесса:
[
p V = \text{const}
]
Где ( V ) — объём газа внутри сосуда.
Точное решение задачи:
-
Нахождение количества молей воздуха в сосуде:
Используем уравнение состояния идеального газа:
[
p_1 V = n R T_1
]
Где ( n ) — количество молей, ( V = S h ) — объём, ( h ) — высота столба газа.
-
Связь между давлением и высотой столба:
При наличии движущегося поршня, изменяется высота столба газа, что влияет на объём и, соответственно, на давление.
-
Скорость выхода газа через отверстия:
Используем уравнение для массового расхода через отверстия при изотермическом процессе:
[
\frac{dm}{dt} = \frac{p_1 \sigma}{\sqrt{2 \pi R T_1 / \mu}}
]
Где ( \sigma ) — общая площадь отверстий.
-
Связь между массовым расходом и изменением высоты поршня:
[
\frac{dm}{dt} = \rho S \frac{dh}{dt}
]
Где ( \rho ) — плотность воздуха внутри сосуда.
-
Плотность воздуха:
[
\rho = \frac{p_1 \mu}{R T_1}
]
-
Соединение уравнений и интегрирование для нахождения ( h(t) ):
Объединяя все вышеперечисленные уравнения, получаем дифференциальное уравнение для ( h(t) ), которое можно интегрировать с начальными условиями ( h(0) = h_0 ), чтобы найти изменение высоты за время ( t = 10 ) секунд.
Заключение:
Таким образом, давления ( p_0 ) и ( p_1 ) определяются следующим образом:
- ( p_0 ) — атмосферное давление снаружи, принимаемое равным ( 10^5 ) Па.
- ( p_1 ) — давление внутри сосуда под поршнем, которое рассчитывается как ( p_0 + \frac{Mg}{S} ).
Используя эти давления и уравнения состояния газа, можно найти изменение высоты поршня за заданное время.
Если вам нужна помощь на каком-либо из этих шагов или более подробное объяснение, пожалуйста, дайте знать!