Съезжающая ледянка и масса снежного кома

[al_ikhan9310 (Alikhan)]

[Alisher (Alisher Yerkebayev)]

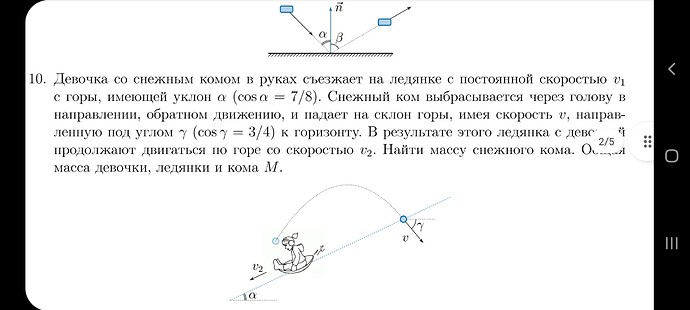
У нас есть две скорости ледянки: до и после броска. Из этого можно сделать некоторые выводы о характере броска снежного кома. Введу угол \beta броска снежного кома под горизонтом и распишу закон сохранения импульса вдоль склона горы:

Mv_1 = (M-m)v_2 - mv_0\cos(\beta-\alpha)

Теперь нужно проанализировать движение снежка, чьё начальное движение было равно v_0. В конце броска угол был равен \gamma, значит компоненты скорости при падении:

v_x'= -v\cos \gamma=const, \qquad v_y' = v\sin\gamma.

Первое уравнение я взял с минусом, так как определил для себя положительное движение вниз и влево. В этом движении меняется только вертикальная компонента скорости, значит законом сохранения энергии можно определить высоту, на которую попал снежок:

\Delta y = \frac{(v_0\cos\beta)^2-v_y'^2}{2g},

а время такого полёта равно

\Delta t = \frac{v_y'-(-v_0\sin\beta)}{g}.

Тогда горизонтальное смещение снежка равно

\Delta x = |v_x'|\Delta t.

Последние два выражения связаны наклоном \tan \alpha = \displaystyle \frac{\Delta y}{\Delta x}. Избавляясь от скоростей и угла \beta, ты найдёшь нужный ответ для массы m.

[Miras (Miras Amirbekov)]

@Alisher

Mv1​=(M−m)v2​−mv0​cos(α+β)

почему cos(a+b)? Мы же рассматриваем движение тело по наклону, как горизонтальное движение

[Alisher (Alisher Yerkebayev)]

да, там \beta-\alpha, спасибо за замечание