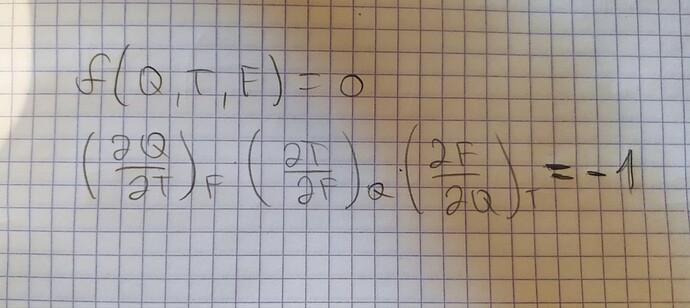Определить изменение температуры плёнки при адиабатическом расширении.
Дайте подсказку пожалуйста, я не совсем понимаю как это делать
1 лайк
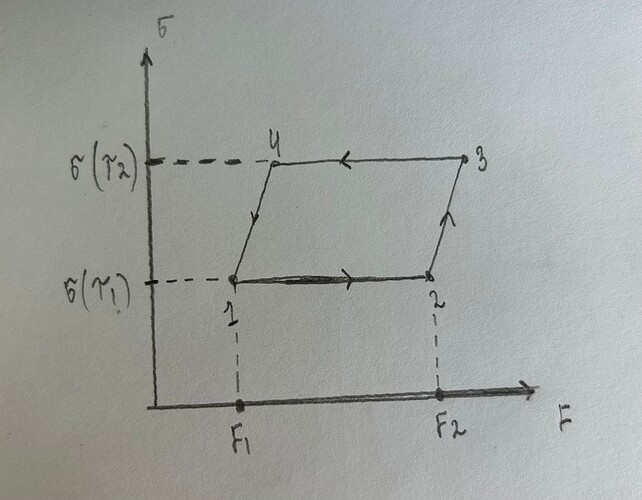
Рассмотри малый цикл Карно (2 адиабаты + 2 изотермы) с малой пленкой жидкости. Причем здесь еще нужно учитывать то, что коэффициент поверхностного натяжения является функцией только температуры \sigma=\sigma(T). Здесь применяя теорему Карно: \frac{A}{Q}=1-\frac{T_2}{T_1}. Дальше ты должен прийти к соотношению q=-\left(\frac{d\sigma }{dT}\right)T. Ну и в конце просто пишешь первый закон термодинамики \delta Q=dU+\delta A для адиабатического расширения
5 лайков
Звучит как подгон, но можно попытаться так:
Скажем что состояние плёнки определяется величинами F, T и Q. Обычно теплоту не берут как параметр состояния. И написать уравнение состояния f(Q, T, F)=0. Для такого уравнение будет выполняться следующее соотношение
Дальше можно подставить туда q и Cf и получить ответ
Скобки с индексом означают что величина в индексе постоянная когда берут эту производную
Доказательство соотношения есть в Сивухине в параграфе 8, Уравнение состояния
P.S.
Если заменить теплоту на энтропию то моё решение будет уже не подгон и норм
6 лайков
я не понял как добить задачу, можно ещё что-нибудь что поможет, пожалуйста
Можно без подгона сделать. Просто вместо тепла поставить энтропию в уравнение состояния. Используя соотношения которые были в том же параграфе Сивухина можно придти к ответу
5 лайков
Почему же? Конечно выражение q=-T\left(\frac{d\sigma}{dT}\right) можно вывести с помощью первого закона термодинамики используя свободную энергию \Psi=U-TS, но выводить ее через рассмотрение бесконечно малого цикла Карно никак не противоречит законам термодинамики и приводит к тому же результату. Если после этого записать первый закон термодинамики для адиабатического процесса \delta Q=dU+\delta A=0. Но мы знаем, что \delta Q=TdS, поэтому dS=0. Для пленки жидкости можно считать что энтропия является функцией температуры и площади самой пленки S=S(T,F), поэтому ее дифференциал:
dS=\left(\frac{\partial S}{\partial T}\right)_FdT+\left(\frac{\partial S}{\partial F}\right)_TdF=0\rightarrow \left(\frac{\partial S}{\partial T}\right)_FdT=-\left(\frac{\partial S}{\partial F}\right)_TdF
Учитывая то, что \delta Q=TdS и C_F=T\left(\frac{\partial S}{\partial T}\right)_F частную производную \left(\frac{\partial S}{\partial T}\right)_F можно записать как \left(\frac{\partial S}{\partial T}\right)_F=\frac{C_F}{T}. Выше мы получили, что q=-T\left(\frac{d\sigma }{dT}\right) и здесь надо учитывать тот факт, что q это теплота на единицу площади при постоянной температуре, q=\left(\frac{\partial Q}{\partial F}\right)_T=T\left(\frac{\partial S}{\partial F}\right)_T. Собирая все это можно получить
\frac{C_FdT}{T}=-\frac{qdF}{T}\rightarrow dT=-\frac{qdF}{C_F}
P.S. Поидее здесь необязательно выводить q=-T\left(\frac{d\sigma }{dT}\right), но наверное для лучшего понимания смысла q стоит попробовать
12 лайков