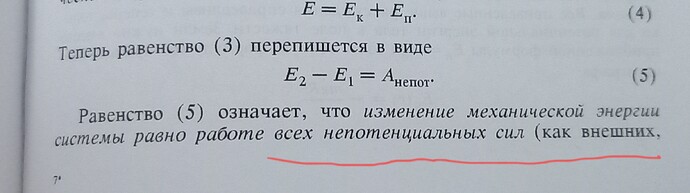В первом случае в Законе изменения мех. энергии говорилось о внешних и внутренних силах, как о непотенциальных. А уже во втором определении внешние силы не определялись как непотенциальные. Т.е там гооворилось о сумме работ “всех внешних сил и непотенциальных внутренних”. Может опечатка? Или я что-то не до понял.
Тут ведь говорится, “в некоторых случаях работу внешних потенциальных сил бывает удобно рассматривать явно, а не выражать через изменение потенциальной энергии”. В таких случаях в механическую энергию системы не входит эта самая внешняя потенциальная энергия.
Т.е, если мы раьоту внешних сил не рассматриваем в виде потенциалтных энергий, то нам все равно какие силы создают эту работу(потенциальные или непотенциальные силы)?
Вообще, да. Изменение внешней потенциальной энергии перейдет в работу внешних потенциальных сил, которая вместе с работой диссипативных (непотенциальных) сил будут составлять работу всех внешних сил.
Можно, например, рассмотреть систему из двух тел, соединенных между собой пружиной, и находящейся на какой-то высоте от земли. Тогда в первом случае полная энергия системы E будет состоять из кинетической энергии тел K, внутренней потенциальной энергии пружины U_i и внешней потенциальной энергии в поле тяготения Земли U_e. Изменение же этой полной энергии будет равным работе диссипативных сил A_д, внутренних и внешних.
E = K + U_i + U_e\\
\Delta E = A_д
Если же принимать второе определение энергии системы, то из первого уравнения упадет U_e, и в этом случае E' = E - U_e.
Из второго уравнения выйдет:
\Delta (E' + U_e) = A_д\\
\Delta E' = А_д - \Delta U_e
А как мы знаем, уменьшение потенциальной энергии равно работе потенциальных сил. A_{п(e)} = -\Delta U_e.
\Delta E' = A_{п(e)} + A_д.
Диссипативные силы можно разбить на внутренние и внешние A_д = A_{д(e)} + A_{д(i)}. А работа внешних сил A_e = A_{п(e)} + A_{д(e)}.
Из этого всего мы получаем уравнение, которое и объясняет мысль автора:
\Delta E' = A_e + A_{д(i)}
2 лайка
Я все же не могу понять зачем тогда нам дабтся два определения Закона изменения мех. энергии, если изменение энергии по итогу является разным(в первом случае ДЕЛЬТА Е(по вашим обозначениям), а во втором ДЕЛЬТА Е’.
Разница лишь в том, что вы берете за систему. Можно взять все тела за одну систему, а можно их мысленно разделить на части. Принципиальной разницы здесь нет. Так же обстоит дело и со внешними полями.
1 лайк