В чем различие между элементарной и бесконечно малой величиной к примеру в первом законе термодинамики d’Q=dU+d’A
dU-бесконечно малое изменение энергии
d’Q,d’A-элементарная теплота и работа
1 лайк
В случае внутренней энергии dU это полный дифференциал, обладающий таким свойством, что интеграл полного дифференциала зависит только от начальной и конечной точки интегрирования и не зависит от пути интегрирования. (\int_1 dU = \int_2 dU). (Exact differential - Wikipedia)
Для работы и теплоты \delta Q, \delta A это неполный дифференциал, для которого интеграл зависит от пути интегрирования. (Inexact differential - Wikipedia)
5 лайков
Можете пожалуйста объяснить что такое неполный дифференциал, а перешел на Википедию , но там непонятно
Вы понимаете разницу между функциями состояния и функциями перехода?
Нет, не очень понимаю
Вообще говоря, дифференциал - это бесконечно малая величина, которая обычно характеризует изменение некоторой величины. Поэтому, чтобы получить дифференциал мы можем взять бесконечно малое изменение некоторой функции dx (полный дифференциал), для которой будет справедлива формула Ньютона-Лейбница (\int dx = x_2-x_1) и его интеграл не будет зависеть от пути интегрирования.
Однако, нас никто не заставлял использовать только выражения типа dx в качесте дифференциала. Мы можем также взять выражения типа Fdx, которые также будут бесконечно малыми и для которых НЕ будет существовать такого f, что df = Fdx. (неполный дифференциал). Примерам подобных выражений являются работа \delta A = PdV и теплота \delta Q = TdS. Для таких выражений интеграл дифференциала будет зависеть от пути интегрирования и \int_1 Fdx \neq \int_2 Fdx.
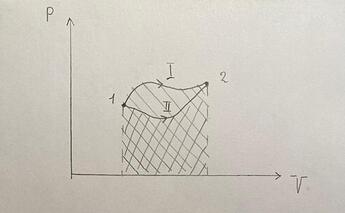
Для наглядного примера можно рассмотреть PV диаграмму идеального газа, на которой два процесса переводят газ из состояния 1 в состояние 2.
В данном случае очевидно, что изменение внутренней энергии для обоих процессов будет одинаковым \Delta U= U_2 - U_1. Однако работа (A = \int PdV), равная площади под графиком процесса, будет различна.
10 лайков
Ты ещё вспомнишь об этих вещах, когда начнёшь изучать термодинамические потенциалы, где начинают применять дифференциал функции нескольких переменных) Для функции F(x, y) её полный дифференциал можно выражать через частные производные по аргументам:
dF(x,y) = \frac{\partial F}{\partial x}dx +\frac{\partial F}{\partial y}dy.
Вся суть заключается в том, что \delta A или \delta Q нельзя выразить в этом виде. Поэтому им просто дают другое слово – элементарная величина.
8 лайков
Большое спасибо