почему среднеквадратичная не равняется v^2 = ikT/m?
я знаю что находят через следующие формулы:
E=mv^2/v
E=ikT/2
тут i берут сразу за 3 равным, но это же справедливо лишь для одноатомной молекулы
Но ведь в среднеквадратичную скорость лишь поступательные движения молекул добавляют. Как ты хочешь добавить вращение вокруг центра тяжести в поступательную скорость?
5 лайков
Дополню то, что сказал Илья:
Допустим энергия какой-то системы зависит квадратично от какой-то переменной х:
E=\psi x^2
Чтобы найти среднюю энергию нужно воспользоваться формулой:
\langle E\rangle=\int\limits_{-\infin}^{\infin} Ef(x)dx
Функция распределения энергии выводится из распределения Больцмана и она выглядит так: (\beta=\frac{1}{kT})
f(x)=\frac{e^{-\beta \psi x^2}}{\int\limits_{-\infin}^{\infin} e^{-\beta \psi x^2}dx}
Дальше если посчитать интеграл сверху выходит довольно простой ответ, который нам очень важен:
\langle E\rangle=\frac{\int \limits_{-\infin}^{\infin}\psi x^2 e^{-\beta\psi x^2}dx}{\int\limits_{-\infin}^{\infin}e^{-\beta \psi x^2}dx}=\frac{1}{2\beta}=\frac{1}{2\beta}=\frac{kT}{2}
Из этого следует то, что вне зависимости от коэф. \psi и самой переменной x сред. энергия равна \frac{kT}{2}, но нужно учитывать что справедливо это только для энергий, которые квадратично зависят от определенного параметра.
Дальше уже все становится легко, найдем степени свободы различных атомов в разных состояниях:
-
Одноатомный газ
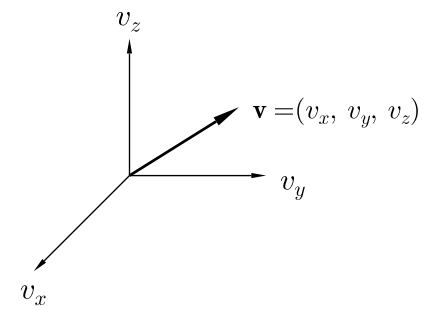
В одноатомном газе естественно может происходить только поступательное движение. Энергия и сред. энергия одного атома:
E=\frac{m\dot x^2}{2}+\frac{m\dot y^2}{2}+\frac{m\dot z^2}{2}\Rightarrow \langle E\rangle=\langle E_x\rangle+\langle E_y\rangle+\langle E_z\rangle=\frac{kT}{2}+\frac{kT}{2}+\frac{kT}{2}=\frac{3kT}{2}
-
Двухатомный газ (в котором не происх. вибрац. движ.)
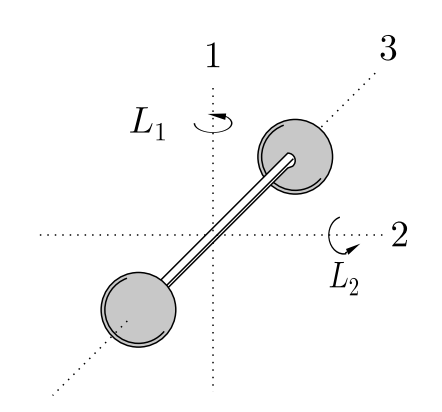
В двухатомном газе, в котором не происходит вибрационных движений могут происходить поступательные + вращательные движения (причем вращение происходит вокруг 2 осей). В этом случае энергия: (момент импульса: L=I\dot \theta)
E=\frac{m\dot x^2}{2}+\frac{m\dot y^2}{2}+\frac{m\dot z^2}{2}+\frac{I_1\dot \theta_1^2}{2}+\frac{I_2\dot \theta_2^2}{2}=\frac{m\dot x^2}{2}+\frac{m\dot y^2}{2}+\frac{m\dot z^2}{2}+\frac{L_1^2}{2I_1}+\frac{L_2^2}{2I_2}
Сред. энерг.:
\langle E\rangle=\langle E_x\rangle+\langle E_y\rangle+\langle E_z\rangle+\langle E_{\theta_1}\rangle+\langle E_{\theta_2}\rangle=\frac{kT}{2}*5=\frac{5kT}{2}
-
Двухатомный газ (в котором есть вибрац. движ.)
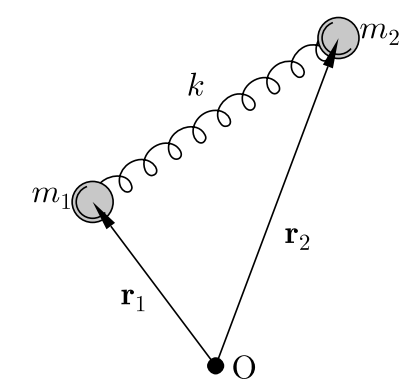
Здесь можно рассмотреть аналогичную систему из двух шаров, связанных пружиной
В этом случае энергия будет равна: (\mu =\frac{m_1m_2}{m_1+m_2})
E=\frac{m\dot x^2}{2}+\frac{m\dot y^2}{2}+\frac{m\dot z^2}{2}+\frac{L_1^2}{2I_1}+\frac{L_2^2}{2I_2}+\frac{k(\vec r_1-\vec r_2)^2}{2}+\frac{\mu(\dot{\vec{r_1}}^2-\dot{\vec{r_2}}^2)}{2}
Средняя энергия:
\langle E\rangle=\langle E_x\rangle+\langle E_y\rangle+\langle E_z\rangle+\langle E_{\theta_1}\rangle+\langle E_{\theta_2}\rangle+\langle E_k\rangle+\langle E_{\mu}\rangle=\frac{kT}{2}*7=\frac{7kT}{2}
Думаю теперь должно быть понятно что в двухатомном и в других многоатомных газах степени свободы добавляются за счет вибрац. и вращ. движений
14 лайков
Ты знаешь, что такое степень свободы?
Степень свободы можно определить как число независимых координат, необходимых для однозначного задания положения системы. В таком случае изменение каждой из этих координат будет представлять собой некую скорость, которая добавляет составляющую в кинетическую энергию системы. Тогда так как на каждую такую составляющую, будет приходиться кинетическая энергия в виде kT/2 (в силу Теорема о равнораспределении — Википедия), то ты получишь соответствующее выражение для полной кинетической энергии молекулы.
6 лайков