пофиксил латех в его ответе
1 лайк
Всего то два года подождать нужно было))
Я имел в виду несколько более короткий и возможно менее строгий вывод. Рассмотрим некий контейнер. Если мы добавим в центр какое-то количество атомов (имеющих не нулевые скорости), через некоторое время они разбегутся по всему объему контейнера.
Если частицы не взаимодействуют друг с другом, состояние слева и состояние справа имеет одинаковую энергию. Тогда что заставляет систему переходить из первого состояние во второе?
Чтобы лучше это понять, нужно провести мысленный эксперимент. Представим, что в контейнере есть перегородка на позиции L, которая может свободно передвигаться.
не сложно заметить, что перегородка будет испытывать некое давление, заставляющее ее двигаться в сторону L_{\max} (совпадающего с границей контейнера). Попробуем описать происходящее математически.
Возьмем сечение контейнера при любом x<L. Наложим на это сечение сетку, размер ячейки которой может вмещать ровно один атом.
Мы можем охарактеризовать одно микросостояние системы если опишем, что происходит в каждой ячейке: пусть будет 1 для “заполнена атомом” и 0 для “пустая”. Полное определение конфигурации требует A\times L значений (где А - площадь сечения).
При фиксированном кол-ве атомов N, в этой конфигурации будет N единичек, и AL-N нулей. Чтобы найти все возможные конфигурации, нужно найти все возможные перестановки одной конкретной конфигурации (A\times L)! и поделить на (AL-N)! (количество нулей, которые неотличимы друг от друга) и на N! (количество единиц). Обозначим кол-во микросостояний за \Omega (L):
\Omega(L, N) = \frac{(AL)!}{(AL-N)!N!} = \frac{1}{N!} AL\times (AL-1) \times\cdots\times (AL-N+1) \tag{1}
когда мы имеем дело с газами, как правило общий объем газа пренебрежительно мал по сравнению с объемом доступного контейнера. Тогда (AL-1)\approx (AL-N+1)\approx AL и:
\Omega(L, N) \approx \frac{1}{N!} (AL)^N \tag{2}
Вообще, строго говоря в общем случае \Omega может зависеть и от внутренней энергии (если между частицами могут быть взаимодействия), но мы допускаем, что все микросостояния имеют одинаковую энергию. Поэтому правильнее всего записать:
\Omega(L, N, U) \approx \frac{1}{N!} (AL)^N \tag{3}
Вспомним определение энтропии через кол-во микросостояний:
S(L, N, U) = k_B \ln \Omega(L) \approx k_B N \ln AL - \ln N! \tag{4}
Вспомним приближение Стирлинга \ln N! \approx N\ln N - N
S(L, N, U) \approx k_B N \ln AL - N\ln N + N = k_B N \left(\ln \frac{AL}{N}+1\right) \tag{5}
Теперь немного фокусов. Возьмем производную энтропии от положения перегородки (остальные переменные постоянны)
\left( \frac{\partial S}{\partial L} \right)_{N,U} = k_B N \frac{1}{\frac{AL}{N}} \frac{A}{N} = \frac{k_B N}{L} \tag{6}
В частных производных есть еще такой фокус, если мы возьмем chain rule по всем трем переменным, их произведение будет равно -1 (triple product rule). Иными словами:
\left( \frac{\partial S}{\partial L} \right)_{N,U} \left( \frac{\partial L}{\partial U} \right)_{N,S} \left( \frac{\partial U}{\partial S} \right)_{N,L} = -1 \tag{7}
Из чего следует:
\left( \frac{\partial S}{\partial L} \right)_{N,U} = - \left( \frac{\partial U}{\partial L} \right)_{N,S} \left( \frac{\partial S}{\partial U} \right)_{N,L} \tag{8}
В сообщении выше, мы определили, что
\left( \frac{\partial S}{\partial U} \right)_{N,L} = \frac{1}{T} \tag{9}
(там вместо L был объем, но поскольку A фиксированная, а V=AL, суть не меняется).
И еще можно вспомнить, что один из способов определения силы – градиент внутренней энергии. А давление – сила на площадь. Т.е.:
- \left( \frac{\partial U}{\partial L} \right)_{N,S} = F = A\times p \tag{10}
Таким образом,
\left( \frac{\partial S}{\partial L} \right)_{N,U} = \frac{A\times p}{T} \tag{11}
Получили два разных выражения для одной и той же производной, они, очевидно, должны быть равны:
\begin{align}
\frac{p\times A}{T} &= \frac{k_B N}{L} \\
p \times (A\times L) &= k_B N T \\
pV &= k_B N T
\end{align}
23 лайка
Хочу добавить про физический смысл статистического определения энторопии и второго закона термодинамики для полноты картины и взаимосвязи .
Начнем немного из далека но надюсь вконце получится прояснить зачем вводится понятие энтропии.
Предисловие
В классической механике (механика которая не задумывается о квантовых и релятивистских явлениях) для каждой из частиц можно написать второй закон Ньютона:
F =m \frac{d^2x}{dt^2}
\qquad (1)
Из уравнения (1) можно заметить что если заменить t \rightarrow-t уравнение не изменяется. Что это значит? Если время течет в обратную сторону закон Ньютона инвариантен при данной трансформации, что означает что направление времени для данного закона не играет никакой роли или другими словами: взяв какое-то состояние тела в какой-то момент времени можно вывести уравнения описывающие как и его будущее так и прошлое. На самом деле все кроме одного закона физики имеют симметрию относительно данной трансформации, в том числе уравнения Шредингера и Максвелла. Отсюда вопрос: Есть ли разница между будущим и прошлым?
Энтропия
Прежде чем ответить на вопрос о времени нужно ввести энтропию.
Возьмем класическое определние энтропии Больтцманна:
S = k_b \log(\Omega) \qquad (2)
Где \Omega количество возможных микросостояний системы при данном макросостоянии. Смысл этого уравнения и значения \Omega уже были расписаны так что не буду повторяться.
Тут важно произнести что в молекулярно кинетической теории есть понятие Броуновского движения (дифузии) или случайного движения частиц внутри газа или жидкости. То есть существует бесконечно повторяющийся случайный процесс.
Согласно закону больших чисел в теории вероятности чем больше раз повторить случайный процесс тем ближе макроскопическая характеристика (среднее значение какого либо измерения всех исходов слуайного процесса) будет к наиболее вероятному исходу. Пример: чем больше раз подкинуть монетку тем ближе будет отношение кол-ва орлов и решек к 1.
Иными словами спустя много взаимодействий системы она приходит в конце к определенному равновесному результату. Но на проведения слуайных процессов нужно время.
Второй закон термоденамики
\frac{dS}{dt} \geq 0
Вот и появляется первый и последний закон в классической физике ассимитричный относительно трансформации t \rightarrow -t. Физический смысл данного уравнения в том что спустя время вероятностная система устремится к состоянию в котором энтропия наиболее высокая что и является определением будущего и прошлого.
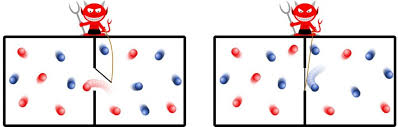
Демон Максвелла
Представим что существует сосуд с перегородкой по середине и также открывающимся отверстием в перегородке. Изначально сосуд находится в равновесном состоянии и температура с обоих сторон перегородки одинаковая а средняя энергия частицы в сосуде равна E_0.
Теперь поставим у данного отверстия маленького демона который будет в левую часть сосуда частицы у которых кинетическая энергия E > E_0 , а для частиц с меньшей чем E_0 энергией он будет закрывать отвертие. Спустя время такая система придет в состояния где температура левой части сосуда больше температуры правой части сосуда. Из уравнения (2) такая система имеет меньшую энтропию чем изначально, что означает что второй закон термодинамики (3) нарушен! На самом деле нет. У демона в голове остаются воспоминания о состоянии каждой частицы которая приближалась к отвертию, из-за этого количество инфомации в голове демона растет и у информации также существует своя энтропия (энтропия Шеннона) не буду углублятся, но простым языком: чем больше информации хранится в обьекте тем выше энтропия Шеннона у этого обьекта
Время
В обыкновенной жизни мы очень часто можем понять что было прошлым а что может быть будущим, так-как у нас есть воспоминания о прошлом но есть лишь вероятностное понимание что произойдет в будущем. С течением жизни мозг человека или запоминает все больше событий или забывает их. Оба этих действия увеличивают энтропию. Как было сказанно ранее всем законам физики все равно в каком направлении течет время, но людям не все равно. Именно по этой причине существует в принципе понятие энтропии. Это метод определения в каком направлении течет время.
6 лайков