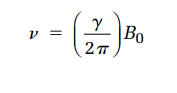А понял, просто индекс 0 отчаянно кричит о том, что это что-то постоянное
Тут стоит кое-что прояснить, что я не сделал и что видимо всех путает, я определил хим.сдвиг не как ИЮПАК, я написал через сравнение с голым протоном \delta(sub)=(\sigma(TMS) -\sigma(sub))\cdot10^6 ИЮПАК считает иначе, но в конце разберемся в чём разница и важно ли это
Для спектрометра CW мы измеряем магнитные поля, при которых у нас наступал резонанс, ну пусть там
B(sub) для образца и
B(TMS) собственно для TMS, тогда можно так посчитать
\begin{gathered}
B=\frac{2\pi v_{RF}}{\gamma \left(1-\sigma \right)} \\
\delta_{CW}=\frac{B (TMS)-B(sub)}{B (TMS)}\cdot10^6= \frac{\frac{1}{1-\sigma_{TMS}}-\frac{1}{1-\sigma_{ref}}}{\frac{1}{1-\sigma_{TMS}}}\cdot10^6 =\\=
\left(\sigma(TMS)-\sigma(sub) \right) \left(1+\frac{\sigma(sub)}{1-\sigma(sub)} \right) \cdot10^6 \cong\left(\sigma(TMS)-\sigma(sub) \right)\cdot10^6
\end{gathered}
Почему я так легко приравнял и забил на \displaystyle \frac{\sigma(sub)}{1-\sigma(sub)} ? Ну, миллионные доли не просто так называются “миллионными” 
Спойлер
Да и знаете, мы изначально выкинули все члены из поляризации более высоких порядков, если начать учитывать это, то придется лезть обратно в первые уравнения и тащить через все формулы второй член разложения \displaystyle B_e(B_0)=-\sigma B_0 + \frac{1}{2} \left.\frac{d^2 B_e}{d B_0^2}\right|_{0} B_0^2+o(B_0^3), а он настолько мал, что приборы даже в теории не имеют такой разрешающей способности и это бессмысленно
Теперь давайте разбираться какое определение хим.сдвига дает ИЮПАК и есть ли существенная разница что именно подставлять в знаменатель
ИЮПАК определяет хим.сдвиг как
\begin{gathered}
\delta = \frac{ \nu_\mathrm{sample} - \nu_\mathrm{ref}}{ \nu_\mathrm{ref}}
\end{gathered}
Частоты измерены в спектрометрах FT, давайте посмотрим, чем отличаются разные варианты определений, выражая их через \sigma
ИЮПАК
\begin{gathered}
\delta = \frac{ \nu_\mathrm{sample} - \nu_\mathrm{ref}}{ \nu_\mathrm{ref}}=
\frac{ B_\mathrm{sample} - B_\mathrm{ref}}{ B_\mathrm{ref}}
=\frac{ B_0(1-\sigma_\mathrm{sample}) - B_0(1-\sigma_\mathrm{ref})}{ B_0(1-\sigma_\mathrm{ref})}
=\frac{ \sigma_\mathrm{ref} - \sigma_\mathrm{sample}}{ 1-\sigma_\mathrm{ref}}
\cong\sigma_\mathrm{ref} - \sigma_\mathrm{sample}
\end{gathered}
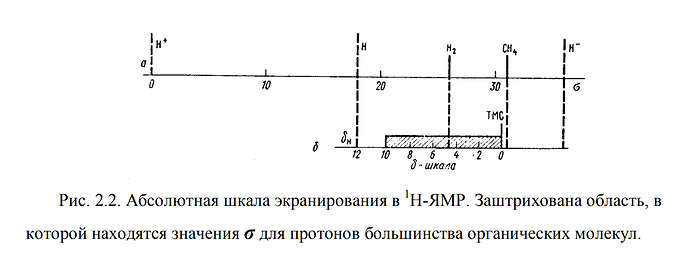
Если за эталон выбрать \ce{H+} то определение ИЮПАК даст нам абсолютные химические сдвиги
\begin{gathered}
\delta_{abs} = \frac{ \nu_\mathrm{sample} - \nu_\mathrm{\ce{H+}}}{ \nu_\mathrm{\ce{H+}}}= \frac{ B_\mathrm{sample} - B_\mathrm{\ce{H+}}}{ B_\mathrm{\ce{H+}}}=- \sigma_\mathrm{sample}
\end{gathered}
Из них легко пересчитать хим. сдвиг ИЮПАК просто вычитая абсолютный сдвиг протона вещества, из абсолютного сдвига эталона (например сдвиг протонов TMS относительно голого протона в районе 30 м.д. а у протонов бензола в районе 22 м.д.)
А в учебниках можно часто встретить такое
\begin{gathered}
\delta = \frac{ \nu_\mathrm{sample} - \nu_\mathrm{ref}}{ \nu_\mathrm{\ce{H+}}}
\end{gathered}
Это всё одно и то же, т.к.
\delta=\frac{ \nu_\mathrm{sample} - \nu_\mathrm{ref}}{ \nu_\mathrm{ref}} \cong
\frac{ \nu_\mathrm{sample} - \nu_\mathrm{ref}}{ \nu_\mathrm{\ce{H+}}}=
\frac{ \nu_\mathrm{sample} - \nu_\mathrm{\ce{H+}}}{ \nu_\mathrm{\ce{H+}}}-\frac{ \nu_\mathrm{ref} - \nu_\mathrm{\ce{H+}}}{ \nu_\mathrm{\ce{H+}}}=\delta_{abs}(\mathrm{sample}) -\delta_{abs} (\mathrm{ref})