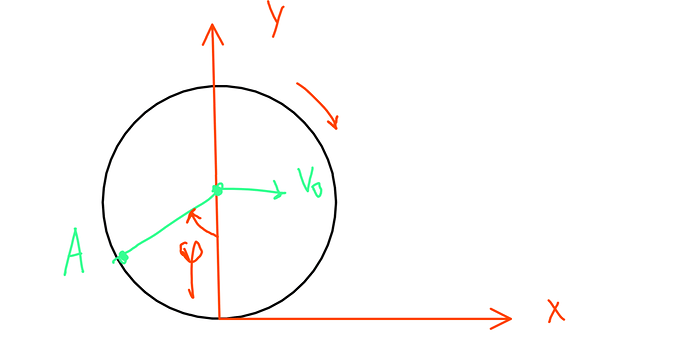
Скажите пожалуйста, где я ошибся промо в ответе 8R, а у меня 4R, и ещё там sin вместо cos
У тебя скорость точки А должно было выйти так:
v_A=2v_0\cos \frac{\varphi}{2}
(посмотри как она выводилась в задаче 1.13, Задача 1.13(Овчинкин))
Скажи пожалуйста какую координатную систему ты взял? (ты неправильно записал координаты)
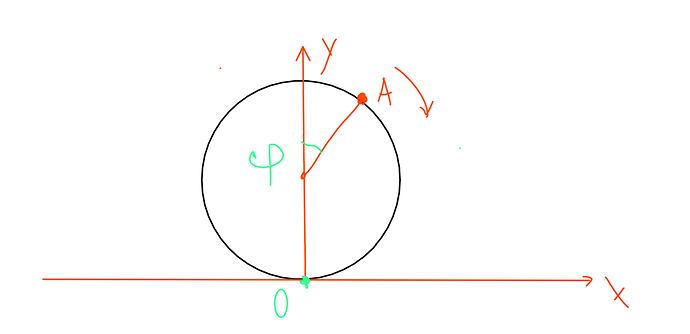
Легче всего взять относительно центра:
x=v_0t+R\sin\varphi, y=R\cos\varphi
Дальше делаешь то же самое, что в твоем решении
2 симпатии
Я вообще взял точку снизу и начал координаты записывать, и у меня так как изначально относительно центра колеса точка идёт влево получилось , то что получилось в первых уравнениях, вроде проверял на разных значениях фи, и вроде получались правдивые результаты
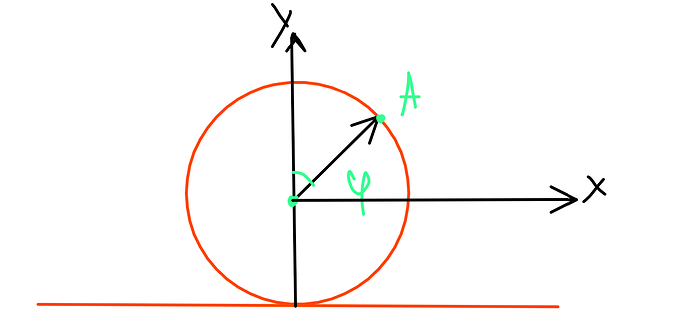
Если ты имеешь ввиду такую координатную систему
То координаты запишутся так:
x=v_0t+R\sin \varphi , y=R(1+\cos\varphi)
Казалось бы ответ тогда будет другим, но если взять производные:
\dot x=v_0+\dot \varphi R\cos \varphi, \dot y =-\dot \varphi R \sin \varphi
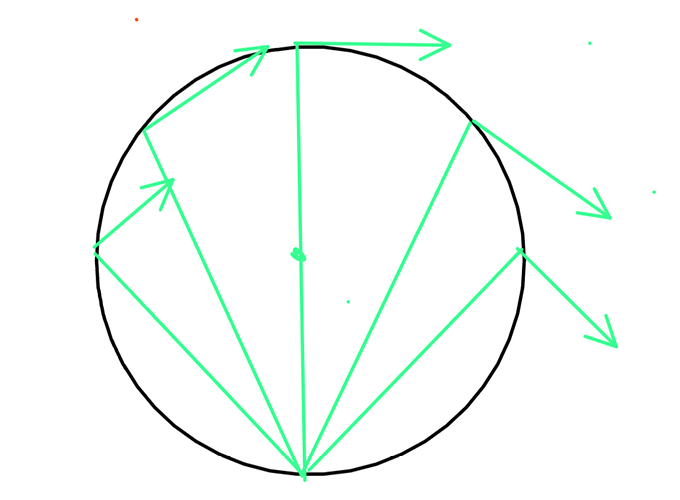
Все точки на ободе колеса вращаются с угловой скоростью \dot \varphi и не движутся поступательно (только вращаются), поэтому они не могут идти влево или вправо
В системе центра скорости точек выглядят так:
\vec v=\vec v_{вращ.}
В системе Земли:
\vec v = \v_0+\vec v_{вращ.}
Ты для х написал x=v_0t-R\sin \varphi, но надо было x=v_0t+R\sin \varphi, потому что \sin\varphi может становиться отрицательным и ты должен писать ее с плюсом
2 симпатии
@Damir, вот как я рассуждал
Допустим наш угол < 180 => sin > 0. И я координату x, точки записал так: x=vt-Rsin(u), т.к первое слагаемое это координата центра колеса, а второе это координата точки отн центра колеса , но точка же идёт в обратную сторону,какое-то время и => если я сделаю +, то получится координата большая, чем на самом деле. Ну итд(надеюсь смог хоть немного объяснить, то о чем думал). Я так понимаю так делать с самого начала было плохой идеей, но почему?
И если сделать x=vt+Rsin(u), то получиться координата большая координаты точки на самом деле
2 симпатии
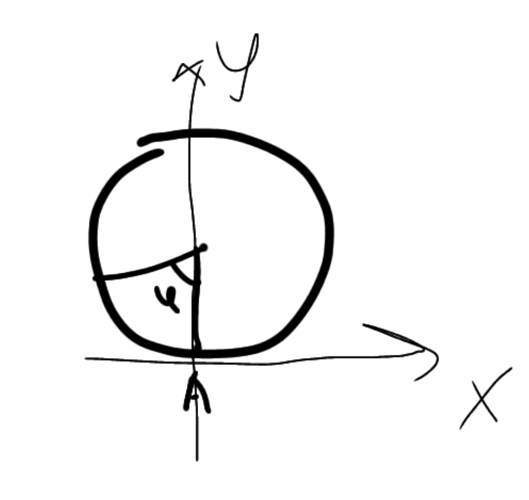
В твоих координатах ты должен считать угол отрицательным: (угол считается против часовой, а диск вращается по часовой):
Тогда твое уравнение:
x=v_0t-R\sin(-\varphi)=v_0t+R\sin \varphi
Дает правильный результат
А вот здесь направление вращение совпадает с направлением отсчета угла:
Значит угол \varphi>0:
x=v_0t+R\sin\varphi
Почему в твоих координатах угол с минусом? Очень просто: то откуда ты считаешь смещено относительно моего на угол -\pi:
x=v_0t-R\sin (\varphi-\pi)=v_0t+R\sin\varphi
Можно общее выражение представить даже так:
x=v_0t+R\sin(\varphi +\varphi_0), y=R\cos(\varphi +\varphi_0)
2 симпатии
Вывод: чтобы в дальнейшем не возникало таких трудностей, отсчитывай угол так, чтобы в начале движения точка имела положительные координаты (\varphi>0, \varphi_0=0)
2 симпатии
Спасибо большое за объяснения, теперь мне стало понятно)
1 симпатия