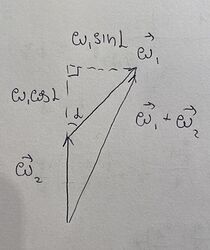
Да, так и есть, однако и сам угол \alpha между векторами \vec \omega_1 и \vec \omega_2 зависит от параметров волчка.
Если ввести сопутствующую систему координат x_1y_1z_1, которая в рассматриваемый момент наклонена по часовой стрелке относительно xyz-координат на угол \alpha (тогда в данный момент \hat x_1 \equiv \hat x), то, вводя момент инерции вдоль оси симметрии волчка I_0 и перпендикулярно ей – I, то момент импульса вдоль этой оси будет равен
\vec L = J\vec \omega,
где J – тензор инерции, который в координатах x_1y_1z_1 имеет вид
J=
\begin{pmatrix}
I &0&0\\ 0&I&0\\0&0&I_0
\end{pmatrix},
а угловая скорость разбивается на компоненты как
\vec\omega = \vec\omega_1+\vec\omega_2 = -\omega_2\sin\alpha\cdot\hat y_1 + (\omega_1+\omega_2\cos\alpha)\cdot\hat z_1 = \\ =
\begin{pmatrix}
0 \\ -\omega_2\sin\alpha \\ \omega_1+\omega_2\cos\alpha
\end{pmatrix}.
Произведение J\vec \omega даёт
\vec L = I_0(\omega_1 +\omega_2\cos\alpha)\cdot\hat z_1 -I\omega_2\sin\alpha\cdot\hat y_1.
Можно преобразовать базисные вектора согласно рисунку: \hat y_1 = \cos\alpha\cdot\hat y -\sin\alpha\cdot\hat z и \hat z_1 = \cos\alpha\cdot\hat z +\sin\alpha\cdot\hat y, и момент импульса в проекциях на xyz будет равен
\vec L = (I_0(\omega_1+\omega_2\cos\alpha)\sin\alpha - I\omega_2\sin\alpha\cos\alpha)\cdot \hat y + (I_0(\omega_1+\omega_2\cos\alpha)\cos\alpha + I\omega_2\sin^2\alpha)\cdot\hat z
Момент сил относительно начала координат xyz появляется из действия силы тяжести и равен
\vec M = \vec r \times m\vec g = -mgr\sin\alpha\cdot\hat x,
этот момент сил изменяет направление вектора \vec L, то есть
\vec M = \vec\omega_2\times \vec L = -(I_0(\omega_1+\omega_2\cos\alpha)\sin\alpha - I\omega_2\sin\alpha\cos\alpha)\omega_2\cdot\hat x = -mgr\sin\alpha\cdot\hat x
Отсюда
\cos\alpha=\frac{I_0\omega_1\omega_2-mgr}{(I-I_0)\omega_2^2}
В условии не было сказано, что угол \alpha считается известным – потому я и сказал, что формулировка условия недостаточна)