Немного не понял, что они тут сделали, вплане, тут химический потенциал 1 и 2 это для растворителей или для растворенного вещества в них?
А у разбавленных растворах у растворенного вещества вообще есть свой химический потенциал, типо допустим у поваренной соли в воде? Ещё не понял как они тут Генри использовали.
Для некоторого соединения С, который распределен между двумя несмешивающимися растворителями 1 и 2.
Да, должен быть.
Предположим, что мы имеем закрытую систему, в которой содержится растворитель А и его пары. Если мы гипотетически добавим какое-то соединение В в систему, и подождем до полного установления равновесия, то мы получим систему, в которой растворенное вещество В будет существовать в равновесии с его же парами. Химический потенциал для газообразного В будет выглядеть следующим образом:
\mu_B(г) = \mu^0_B(г) + RT\ln \frac{p_B}{p^0}
Поскольку газообразный В находится в равновесии с растворенным В, можно сказать, что \mu_B(г) = \mu_B(ж). Также, по закону Генри p_B = Kx_B, где x_B - мольная доля соединения В в растворе. Поэтому,
\mu_B(ж) = \mu^0_B(г) + RT\ln \frac{Kx_B}{p^0} = \mu_B^0(г) + RT\ln \frac{K}{p^0} + RT\ln x_B
Здесь можно сказать, что \mu_B^*(ж) = \mu_B^0(г) + RT\ln \frac{K}{p^0}. Тогда в конечном итоге получается, что
\mu_B(ж) = \mu_B^*(ж) + RT\ln x_B
Но тут стоит отметить, что закон Генри согласуется с экспериментальными наблюдениями только при определенных условиях (каких?), и поэтому, использовать вышеприведенное выражение для химического потенциала растворенного вещества не совсем корректно использовать, когда, например, у тебя имеется довольно значительное количество
(почему?), и поэтому вместо мольной доли, концентрации, давления, мы используем активности.
1 лайк
Но почему они взяли, что химический потенциал чистого С разный в двух фазах? Ещё ведь эти 2 растворителя образуют два отдельных слоя, в которых один слой снизу,а другой сверху, и так вот, может ли раствор снизу образовать пары и быть с ними в равновесии?
Когда раствор идеально разбавленный, а-ля в нем доля растворенного вещества стремится к 0.
Ну видимо выбора особо-то и не было, разве что Закон Рауля, но тот только для растворителей в идеально-разбавленных растворах, а нам они не интересны, поскольку не смешиваются и не находятся в равновесии.
А вы понимаете что такое химический потенциал?
Парциальная энергия Гиббса, способность вещества совершать физико-химические явления
1 лайк
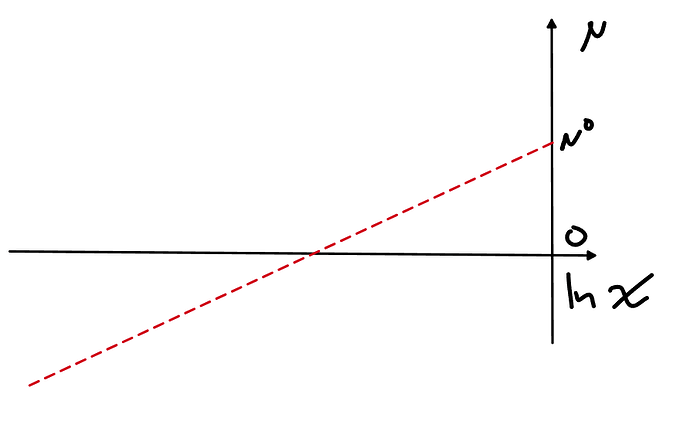
Как и у энергии Гиббса, для стандартных потенциалов можно выбирать разные удобные для нас точки отсчёта, например ситуацию, где стандарт принят за чистые вещества называется “симметричная система сравнения”.
А тут “нессимитричная система сравнения” за стандартное состояние принято бесконечно разбавленное состояние. Разницу между ними можно с помощью константы Генри найти
Немного не понял, значит для разных растворов разные константы Генри, даже если растворенное вещество одно и тоже? И это единственный фактор из за которого химический потенциал чистого С разный? Блин хотя с другой стороны, чистый на то и чистый, что должен иметь лишь одно единичное значение, ведь типо его доля 100%.
Это не хим. потенциал чистого вещества
Почему? Обычно так и обозначают хим потенциал чистого вещества, со штукой *.
Так, ладно давай тогда придумаем и разберем пример неидеального раствора. Начнем с идеального… Для него молярная энтальпия смешивания это 0, а молярная энтропия смешивания и молярная энергия Гиббса смешивания зависит от мольной доли первого компонента как
\begin{gathered}
\Delta_fS_m=-R \left[ x_A \ln x_A +x_B \ln x_B \right]=-R \left[ \left(1-x\right) \ln \left(1-x \right) +x \ln x \right] \\ \\
\Delta_fG_m=-T\Delta_fS_m=RT \left[ \left(1-x \right) \ln \left(1-x \right) +x \ln x \right]
\end{gathered}
В идеальном растворе хим.потенциал первого компонента у нас от логарифма мольной доли зависит обычным образом
\mu_A=\mu_A^\circ+RT\ln x_A
Молярная энергия Гиббса идеального раствора тогда
\begin{gathered}
G_m= \frac{n_A\mu_A+n_B\mu_B}{n_A+n_B}= \\
=
x_A \biggl( \mu_A^\circ+RT\ln x_A
\biggr) +
x_B\biggl( \mu_B^\circ+RT\ln x_B
\biggr)
=
\\
=x_A\mu_A^\circ +(1-x)\mu_B^\circ+ RT \Bigl[ \left(1-x \right) \ln \left(1-x \right) +x \ln x \Bigr]
\end{gathered}
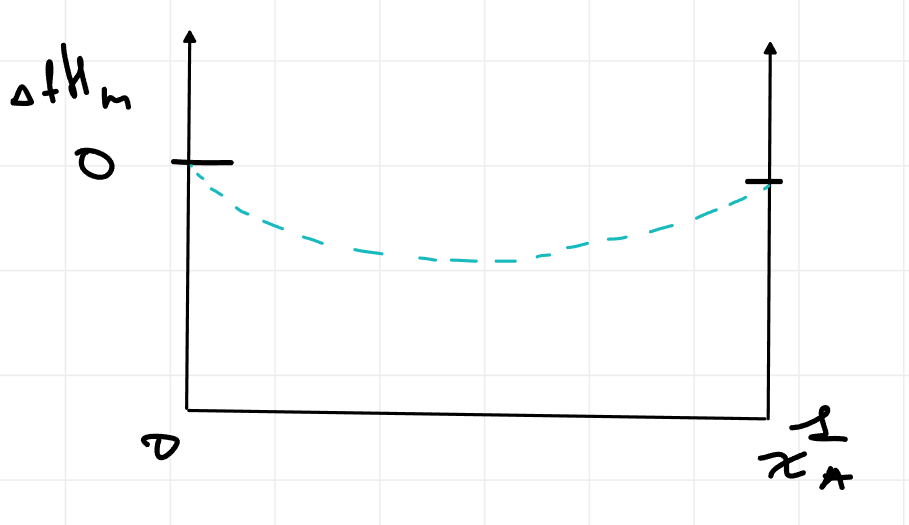
Сделаем раствор неидельным, трогать энтропию я не буду, давай представим что у нас выделяется тепло при смешивании A и B, возьму просто параболу для энтальпии смешивания
\Delta_fH_m=-C x_A x_B=-Cx_A(1-x_A)
На краях 0, т.к. если мы смешиваем чистое A с другой порцией A, не ожидаем что у нас тепло будет выделяться
Тогда что у нас получается теперь? Молярная энергия Гиббса смешивания тогда
\Delta_fG_m=\textcolor{blue}{ \hbox{$\Delta_fH_m$}} -T\Delta_fS_m = \\
= \textcolor{blue}{ \hbox{$-Cx_A(1-x_A)$}}+ RT \Bigl[ \left(1-x \right) \ln \left(1-x \right) +x \ln x \Bigr]
Молярная энергия Гиббса раствора тогда
G_m
= -Cx_A(1-x_A)+x_A\mu_A^\circ +(1-x)\mu_B^\circ+ RT \Bigl[ \left(1-x \right) \ln \left(1-x \right) +x \ln x \Bigr]
А энергия Гиббса раствора вообще
G=(n_A+n_B)G_m=-C\frac{n_An_B}{n_A+n_B} +n_A\mu_A^\circ +n_B\mu_B^\circ+ RT \left[ n_A \ln \left(\frac{n_A}{n_A+n_B}\right) +n_B \ln \left( \frac{n_B}{n_A+n_B}
\right) \right]
Т.е. вся неидеальность находится в \displaystyle-C\frac{n_An_B}{n_A+n_B}
Теперь найдем хим.потенциал первого компонента, по определению это \displaystyle \left(\frac{\partial G }{\partial n_A }\right)_{T,p,n_B,}
Ну берем производную получается
\mu_A=\mu_A^\circ+RT\ln x_A - C\left(1-x_A \right)^2 = \mu_A^\circ-С+RT\ln x_A +2Cx_A -Cx_A ^2
При малых мольных долях A, у нас последние слагаемые почти исчезают
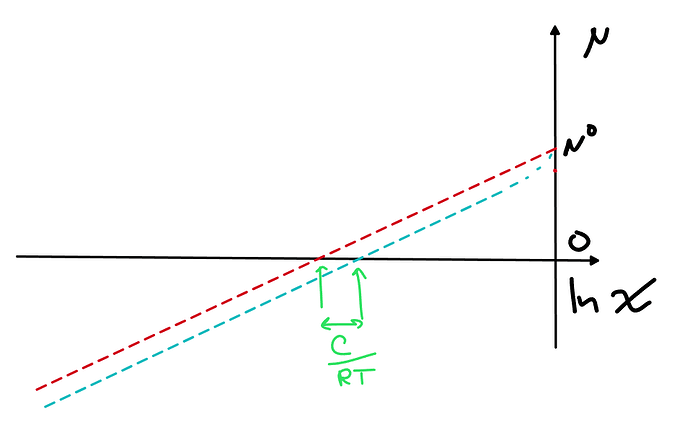
Поэтому график теперь выглядит так
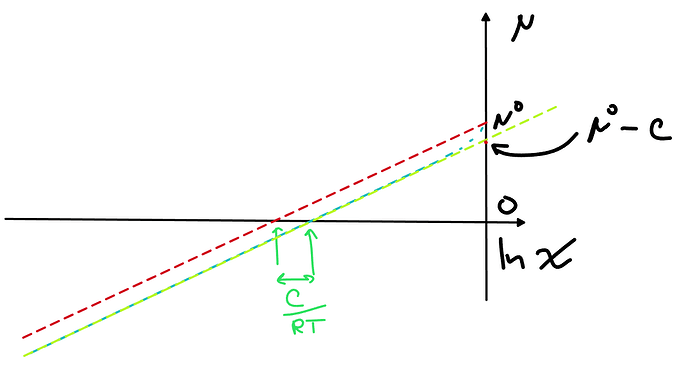
При малых мольных долях у нас просто теперь хим.потенциал идет практически параллельной линией под линией идеального раствора, поэтому очевидно, хочется просто сдвинуть точку отсчета, т.е. поменять стандартное состояние с чистого компонента на что-то другое, тут сразу бросается в глаза, что удобнее всего будет взять \mu^*=\mu^\circ-C, тогда для малых мольных долей A можно будет написать
\mu_A \approx \mu_A^\circ-С+RT\ln x_A =\mu_A^*+RT\ln x_A
Новое уравнение желтая линия на графике
Вопрос к тебе, как из моей модели можно достать константу Генри?
4 лайка
Я тут уже поплыл, что вы берёте за С, и откуда эта формула энтальпий?
μ_A=μ_A^∘ + RTln(x_{A})
Вы тут μ_A^∘ за стандартный потенциал приняли или чистый?
Вроде как должен быть чистый, но в учебнике, что я читал чистый писали как: μ_A^*
Типо там было так, если стандартный, то:
μ_A=μ_A^∘ + RTln(p_A)
Если чистый, то:
μ_A=μ_A^* + RTln(x_A)
Просто константа, формулу сам придумал, надо было как-нибудь поломать идеальность, это самое простое и первое что пришло в голову, просто для демонстрации придумал
А че так можно было? А нельзя было взять как тупо \Delta H, где оно не равно 0. Кстати, а при смешении идеальных веществ энтальпия равна 0, но почему так? Просто так приняли? А если не идеальные, то что мы должны учитывать из того, что влияет на энтальпию?
Идеальные вещества это что? Те кто друг с другом не взаимодействуют никак вообще. А теплота откуда выделяется/поглощается? С каких-нибудь взаимодействии (химические или физические). А тут то таких нет.
Я думаю отсюда вы поймете ответ на свой второй вопрос
Можно, но было бы слишком обще, графики не порисуешь особо, и надо было чтобы на краях было 0
Я сейчас загуглил, я велосипед придумал, оказывается это называется моделью Хилденбранда, он выводил её из предположения, что у него две неполярные жидкости смешиваются, и там только Ван-дер-Ваальсовы силы действуют. Хорошо описывает раствор йода в алканах.
Идеальные вещества? Впервые слышу такой термин, вы имели ввиду образование идеального раствора. При образовании идеального раствора энальпия 0, об этом точно писали в учебнике, ведь это основы. Почему так, подумайте над этим сами.
1 лайк
После этого момента тоже не особо понятно, как вы это сделали, вернее чего конкретно взяли производную.
Ну это я примерно понял, но всегда думал, что это для всех, а не только идеальных, типо допустим смешали просто два вещества и они образовали не идеальный раствор, и энтальпия откуда берется? Может из за новых водородных связей или чего-то подобного?
Энергии Гиббса… вы когда отвечали мне и писали “парциальная энергия Гиббса” вы же понимали что означает “парциальность”?
Типо энергия Гиббса какого-то компонента на общую энергию Гиббса. Вы взяли производную энергии Гиббса раствора? Эхх, немного поплыл.
Парциальная величина Z i-го вещества это
\overline{Z_i}=\left(\frac{\partial Z }{\partial n_i }\right)_{p,T,n_{j \neq i} }
Это определение парциальных величин
А нельзя тогда назвать это молярной величиной?