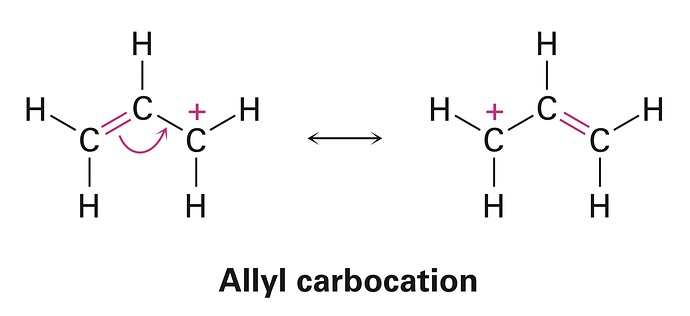
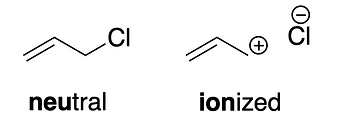Давно хотел спросить, почему аллильная связь такая слабая? Имею ввиду да, если ее сломать то образуется радикал или карбокатион, который стабилизируется резонансом, однако откуда молекула до разрыва связи знала об этом? Откуда она знала, что выгоднее всего сломать связь С-Н рядом с двойной связью и сделала ее слабее, и как она могла сделать ее слабее? Имею ввиду есть две C-H связи, но одна из них слабее, хотя по всем пораметрам они одинаковы.
Я думаю:
Если допустить, что депротонирование обратимо, то в конце будет равновесие. А преобладать будет самый стабильный продукт. А стабильный у нас – аллильный катион.
Связь становится слабее, т.к. энергия, необходимая на разрыв связи будет меньше, из-за более стабильного катиона. То есть молекула ничего не знала, и не делала слабее, просто требуется больше энергии на отрыв простого протона, в то время как отрыв аллильного протона будет энергетически частично “компенсирован” резонансной стабилизацией
То есть мы, чтобы разорвать связь к примеру вложили 100 Дж, а со стабилизацией вернулось 10 Дж, а нельзя сразу 90 Дж вложить и все?
я думаю это не так работает, допустим, энергия связи 400 кдж то есть молекуле не выгодно разрывать эту связь на 400 кдж, и мы должны ей эту энергию сообщить. Однако если в результате образуется стабильный катион, то молекуле будет не выгодно например уже не на 400 а только на 370 кдж, тогда и энергия которую надо приложить уменьшается, ну и связь становится слабее
Значит мы вкладываем 400 кДж а получаем 30 кДж так? Или же сразу молекула решила дать этой связи 370 кДж?
нет, я думаю он имел ввиду что стабильному катиону уже не выгодно разрываться на 400 кдж( мы не выкладываем ее и не получаем 30 кдж)а просто энергия разрыва уменьшается.
нет, вот допустим есть график энергии, и вот обычный катион будет выше на 400 кдж, а стабильный будет выше только на 370 кдж, соотвественно надо приложить 370 кдж энергии на разрыв связи(1 моля в-ва)
Хороший вариант.
Нет, зачем? Просто если одна связь слабее другой, на ее разрыв нужно меньше энергии. Соответственно, скажем, если условное основание обладает (каким-то образом, например термальной) энергией 90 Дж, то оно сможет сломать только связь в 90 Дж, и не сломает 100 Дж.
На самом деле вопросы @Sanjaster скорее про “почему аллильная связь слабее обычной”, т.е. нам надо объяснить почему условные 90, а не 100.
Вообще, отвечая на вопрос «как молекула знает», я бы предложил такую гипотезу[1].
Давайте сравним хлорпропан (reg) и 3-хлорпроп-1-ен (allyl). У каждого можем нарисовать две гипотетические формы:
Можно предположить, что истинная структура молекулы – линейная комбинация двух форм[2]
Чем больше значения c_2, c_4 тем больше вклад ионизированной формы. При этом, сами значения этих коэффициентов будут больше в том случае, когда ионизированная форма менее нестабильна по сравнению с нейтральной. Думаю вы согласитесь, что в ионизированной форме резонансная стабилизация понижает энергию фрагмента.
В итоге, мы предполагаем, что c_2 < c_4. Мы знаем[3], что любые свойства молекул описываются волновой функцией. Если в \Psi_{allyl} больше вклада \phi_{ion}, то логично предположить[4], что энергия связи в 3-хлорпроп-1-ене будет меньше, чем в хлорпропане, где вклад \phi_{ion} меньше.
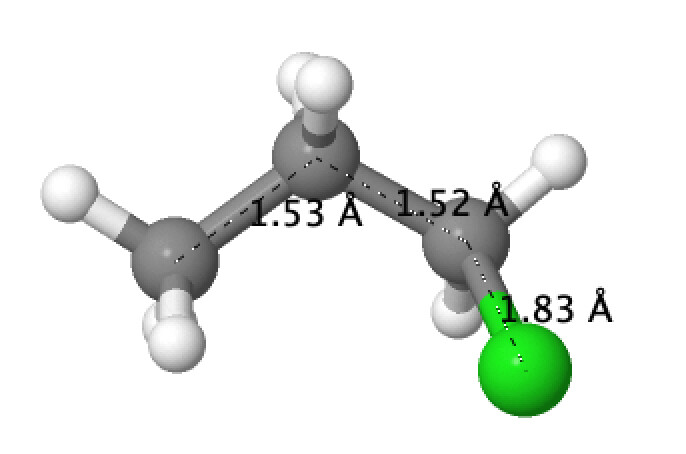
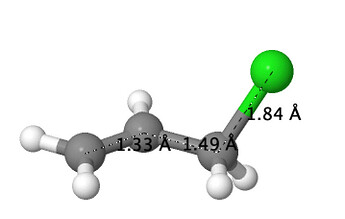
Я решил попробовать проверить гипотезу. Давайте посмотрим на длины связей в двух молекулах:
Что мы видим?
- C(sp2)-C(sp3) связь короче C(sp3)-C(sp3) (1.49 \AA против 1.52 \AA). Незначительно, но короче.
- В аллильной структуре C-Cl чуть длиннее 1.84 \AA против 1.83 \AA. Незначительно, но длиннее.
Помимо этого, порядок связи в 3-хлорпроп-1-ене (0.9366) чуть меньше, чем в хлорпропане (0.9378).
Иными словами, наше предположение, что c_2<c_4 может быть оправдано
Меня тоже довольно часто мучают вопросы «а откуда молекула знает» и ничего внятного в ответ кроме “math works out” я не получал. А сейчас, кажется, наконец-то я сам понял. ↩︎
Та же идея, что и с резонансным гибридом ↩︎
Из постулатов квантовой механики ↩︎
Грубо говоря, энергия связи в \phi_{neu} в обоих случаях равна некому значению x, а энерегия “связи” (энергия необходимая на разрыв ионной пары) в $\phi_{ion} равна y, при этом y \ll x . Энергия связи \Psi_{reg} будет равна c_1^2 \cdot x+c_2^2 \cdot y, а у \Psi_{allyl} она будет равна c_3^2 \cdot x+c_4^2 \cdot y. Поскольку c_4>c_2 (что одновременно подразумевает c_1 > c_3 ), энергия связи в аллильной форме будет меньше, чем в обычной. ↩︎
А разве при стабилизации энергия не выделяется? Имею ввиду если сила аллильная связи скажем 370 кДж, мы вложили столько энергий, и когда образовался карбокатион, он немного стабилизировался и ещё дополнительно выделил энергию?
Давайте сначала разберемся с математикой.
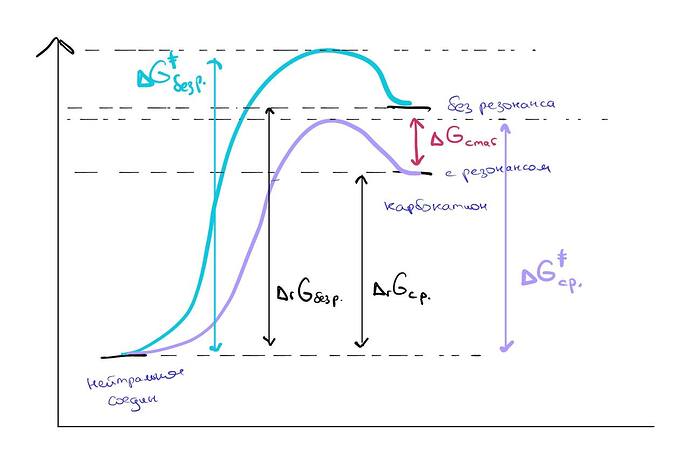
Все обозначения на графике понятны?
Энергия связи – это \Delta_r G_{без\, р} и \Delta_r G_{с\, р}
Стабилизация резонансом это \Delta G_{стаб}
С графиком согласны?
Это самое главное.
Теперь, ваш первоначальный вопрос был почему \Delta_r G_{без\, р} > \Delta_r G_{с\, р}. Ответ я на него дал выше.
Теперь самое главное, что надо понимать про термодинамику[1] – она дает статичную картину. Она не говорит КАК происходит процесс. Она только говорит: вначале была такая молекула, стала такой. Между ними разница \Delta_r G_{с\, р}.
А как эта разница образуется – в рамках термодинамики можно придумать самые разные интерпретации. Можно просто сказать: молекуле дали \Delta_r G_{с\, р} и все.
Можно сказать молекуле дали \Delta_r G_{без\, р} а она потом отдала \Delta G_{стаб}.[2]
а можно вообще вспомнить нашу дискуссию