Angular Velocity of a Pendulum

Физика Механика
1

If the total mass of the particles is m, and the center of mass is moving at velocity v_{cm}, the momentum of the system is: p=mv_{cm}

Могу ли я тогда сказать, что кинетическая энергию системы можно выразить через линейную скорость центра масс как KE=\frac{1}{2}mv_{cm}^2?

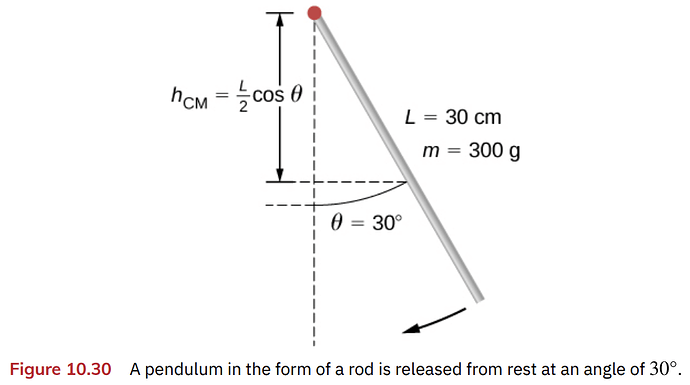
A pendulum in the shape of a rod (Figure 10.30) is released from rest at an angle of . It has a length 30 cm and mass 300 g. What is its angular velocity at its lowest point?

image
image964×539 52.4 KB

Ранее в книжке писали, что угловая скорость удобна тем, что она везде одинаковая. Почему нельзя найти линейную скорость центра массы и поделить её на расстояние от центра массы до оси вращения маятника, чтобы найти угловую скорость на конце маятника?

2

Для какой-либо системы нужно еще учитывать кинетическую энергию движения частиц относительно их центра масс (см. Теорема Кёнига). Для маятника в виде стержня это будет следующим.

K = \frac{1}{2}mv_{cm}^2 + \frac{1}{2}I_{cm}\omega^2

Здесь I_{cm} – это момент инерции стержня относительно его центра масс.

Можно.

1 лайк