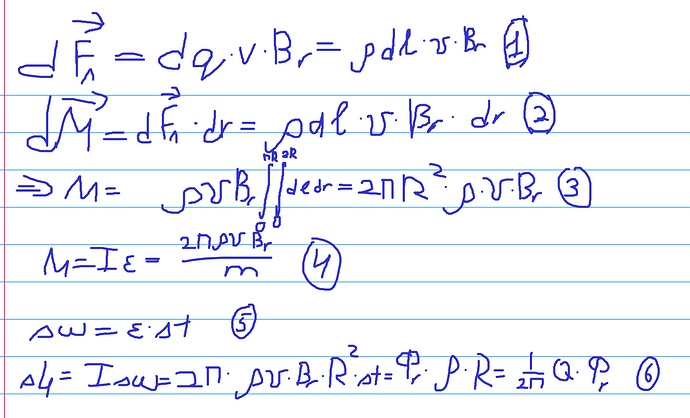Доказательство пропорциональности приращение момента импульса к приращению потока магнитной индукции
изменения магнитного поля → изменение потока → появление эдс индукции в контуре/вихревого электрического поля в пространстве
-Можно заметить, что только радиальная часть индукции \vec B_r вносит вклад в силу Лоренца в начале. Нарисовать куда она направлена → увидим, что она начинает раскручивать кольцо.
-Когда кольцо немного раскрутилось, теперь посмотрим вклад \vec B{\tau} - эта проекция только затармаживает поступательное движение кольца.
увидим, что она начинает раскручивать кольцо
именно движение зарядов по окружности здесь считается током
ЭДС индукции выразим двумя способами
\epsilon_i = \frac{\Delta \Phi}{\Delta t} = E * 2\pi R
Напряженность вихревого поля
E = \frac{1}{2\pi R}\frac{\Delta \Phi}{\Delta t}
Сила, действующая на итый заряд
F_i = q_iE
Момент, который он вкладывает
\tau_i = F_iR = q_iER
Суммарный момент
\tau = \sum\tau_i = ER\sum q_i = qER = \frac{q}{2\pi}\frac{\Delta \Phi}{\Delta t}
Осталось написать уравнение моментов
\Delta L = \tau \Delta t = \frac{q}{2\pi}\Delta \Phi
5 лайков
я в 4 забыл сказать что там угловое ускорение равно тому что там выражено через плотность, магнитную индукцию и тд
Ну 2, 3 подогнал кжс. Плечо там всегда постоянно - радиус кольца, задача впрнц решается без анализа, немножко путаешься в обозначениях(
2 лайка