Всем салам, сижу, чалю Сивухина первый том и тут такая тема:
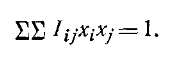
Сивухин че-то на объяснения поскупился. С какого-то перепугу он взял
ниче не понял. Как он так сделал, да и размерности не сохраняются, да и на кой черт он нужен?
Прошу помочь, заранее спасибо
1 лайк
А можно параграф, в котором это было?
53 параграф
1 лайк
Обрати внимание на вывод формулы (53.1), т.е.
I = I_{xx}s_x^2 + I_{yy}s_y^2 + I_{zz}s_z^2 + 2I_{xy}s_xs_y + 2I_{yz}s_ys_z + 2I_{xz}s_xs_z = \sum^3_{i, j=1} I_{ij}s_is_j.
В краткой записи суммы сделали условную замену индексов x=1, y=2, z=3, чтобы сумму можно было записать.
А теперь сопоставь этот факт с каноническим уравнением поверхности второго порядка
a_{11}x^2 + a_{22}y^2 + a_{33} z^2 + 2a_{12}xy + 2a_{23}yz + 2a_{13}xz + 2a_{14}x + 2a_{24}y + 2a_{34}z + a_{44}=0.
Это страшилище немного облегчается тем, что предпоследние 3 коэффициента равны нулю, а самый последний a_{44} есть аналог -I:
-a_{44} = a_{11}x^2 + a_{22}y^2 + a_{33} z^2 + 2a_{12}xy + 2a_{23}yz + 2a_{13}xz = \sum^3_{i, j=1}a_{ij}l_il_j.
Вот тут я произвёл условное обозначение l_1=x, l_2=y, l_3 = z.
Общий смысл такой аналогии кроется в том, что момент инерции твёрдого тела имеет некоторое сходство с уравнением поверхности второго порядка (частным случаем которого является эллипсоид). Иначе говоря, если первую сумму разделить на I и “раскидать” его по s, то можно сделать такую замену
x_i = \frac{s_i}{\sqrt I}, \quad x_j=\frac{s_j}{\sqrt I}.
Тогда получим
\frac{1}{I}\sum^3_{i, j=1} I_{ij}s_is_j = \sum^3_{i, j=1} I_{ij}\left(\frac{s_i}{\sqrt I}\right)\left(\frac{s_j}{\sqrt I}\right) = \sum^3_{i, j=1} I_{ij}x_ix_j = 1
И как раз эта последняя сумма, нормированная к единице, показывает уравнение эллипсоида (что-то вроде \displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1, но должны добавиться ещё слагаемые, содержащие xy, yz, xz, потому что для общего случая мы не совмещаем направления полуосей с направлениями координат). Для такого эллипсоида можно в любую точку проводить вектор \vec r = \displaystyle\frac{1}{\sqrt I}, и его длина (тут мы реально уходим от типичного понятия размерности длины) зависит от направления, величина которой как раз диктуется значением I в зависимости от направления.
Сивухин как всегда всё усложнил и не пояснил доступным языком)
7 лайков
емааа, че за жесть. Большое спасибо за пояснение!