Express the vector SX in terms of a and b

[arujean (Aruzhan Tokhtarova)]

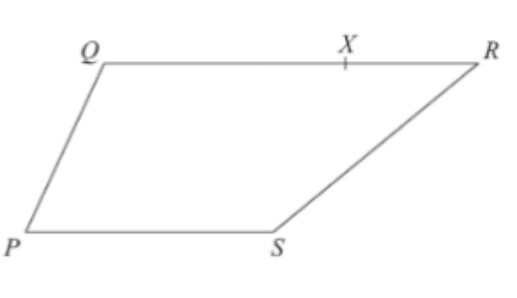
Express the vector SX in terms of vectors PQ=a and PS=b, if QX:XR=3:1 and PS= \displaystyle\frac{1}{2} QR.

A. - \displaystyle\frac{1}{2}b-a
B. \displaystyle\frac{1}{2}b+a
C. - \displaystyle\frac{3}{2}b+a
D. \displaystyle\frac{3}{2}b-a

Добрый вечер, ребята. Как решать такую задачу? Не знаю с чего начать и в целом как решать такого рода задачи на векторы. Помогите, пожалуйста.

[KimTimur]

\overrightarrow{PQ} = \vec{a},\qquad \overrightarrow{PS} = \vec{b}

\overrightarrow{SX} можно будет выразить как вектор если представить, частью какого треугольника он может являться. Тогда, воспользовавшись правилом сложения векторов, можно будет прийти к ответу.

\begin{equation} \Delta{PSX}:\quad \overrightarrow{PS} + \overrightarrow{SX} =\overrightarrow{PX} \end{equation}

Отсюда нам неизвестен вектор PX, для этого можно рассмотреть другой треугольник:

\begin{equation} \Delta{PQX}:\quad\overrightarrow{PQ} + \overrightarrow{QX} = \overrightarrow{PX} \end{equation}

Остается только выразить вектор \overrightarrow{QX}. Это можно сделать из данных в условии соотношений:

\overrightarrow{QX} = \frac{3}{4}\overrightarrow{QR} = \frac{3}{4}\cdot2\overrightarrow{PS} = \frac{3}{2}\vec{b}

Приравнивая (1) и (2):

\vec{b}\; + \overrightarrow{SX} = \vec{a}\; + \frac{3}{2}\vec{b}

\overrightarrow{SX} = \vec{a}\; + \frac{1}{2}\vec{b}

[quaton (Daniel Tyulyubayev)]

Я бы рассмотрел сразу четырехугольник PQXS, потому что это проще и не нужно вводить \overrightarrow{PX}.

\overrightarrow{PQ}+\overrightarrow{QX}-\overrightarrow{SX}-\overrightarrow{PS}=0 \\ \overrightarrow{SX}=\overrightarrow{a}+\overrightarrow{QX}-\overrightarrow{b}

Потом также выражаем \overrightarrow{QX} и находим ответ.