Химия → IChO → 2005 | BeyondOlympiads

[Sammael (Илья)]

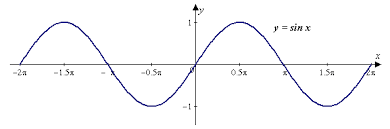
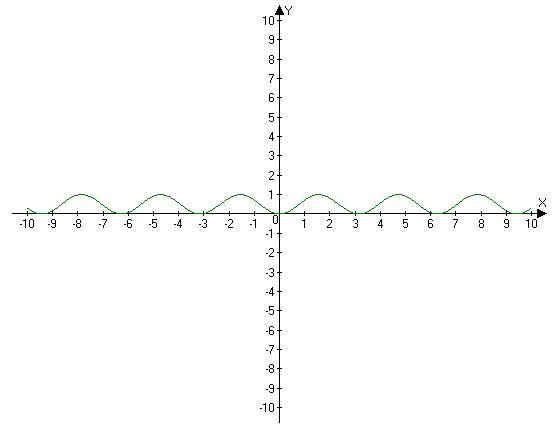
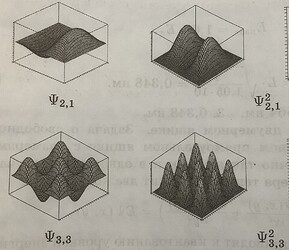
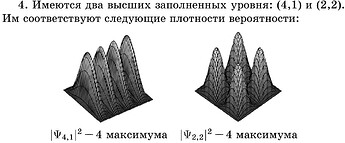
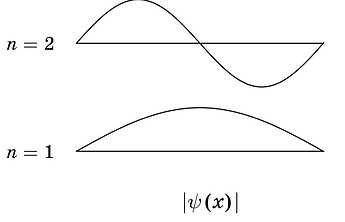
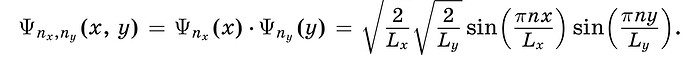Можно брать производную, а можно просто вспомнить как выглядят функции \sin(x)\ \sin^2(x) \cos(x) \ \cos^2(x) и где у них максимумы а где нули (узлы)

Собственно поэтому я и подумал, что вам не хватает базы по математике. В школьной программе ученики очень долго рисуют графики разных функций, сначала по точкам, потом изучают как влияет на график функции разные модификации изначальной функции, а набив руку уже видя уравнение ты понимаешь как выглядит график. Если функция f(x,y) имеет вид \sin^2(ax)\sin^2(by) можно конечно производные брать и уравнивать к нулю, но вообще конечно в идеале это должно быть очевидно где у неё максимумы и как выглядит график подобной функции. Если вы будете прилагать усилия, то со временем это вам станет очевидно.

[Anton (Anton Morgunov)]

@Sanjaster

Можете показать решение 4 пункта?

Этот пункт — самая прямая проверка навыка анализа функции. Уровень сложности — задача на закрепление пройденной темы. Если вы изучите анализ функций, вы сможете ответить на вопрос в этом пункте.

@Sanjaster

Возможно я и пойму,

Вы сами еще не поняли, что если вы смотрите в решения не для того чтобы проверить ваш ответ, а для того, чтобы понять как решать, вы не поймите и не запомните абсолютно ничего?

[Sanjaster (Калиакбар Санжар)]

@Sammael

Можно брать производную, а можно просто вспомнить как выглядят функции sin⁡(x) sin⁡2(x)cos⁡(x) cos⁡2(x)\sin(x)\ \sin^2(x) \cos(x) \ \cos^2(x)sin(x) sin2(x)cos(x) cos2(x) и где у них максимумы а где нули (узлы)

Я кажется начинаю понимать, ведь волновые функции частиц это ведь просто функций от синуса:

Типо вот этого. Сама по себе это функция вроде ничего не дает, но ее квадрат(хз зачем модуль, может от мнимых чисел?) даёт

Даёт что-то типо этого, где есть только узлы(y = 0) и максимумы, или же точки где вероятность нахождения электрона выше всего.

В 4 пункте нас просят найти эти максимумы для уровней (4,1) и (2,2)
И для этого нам нужна эта формула:

По сути нам известно все, кроме х и y, вернее мы знаем только их границы, а дальше уже без понятия как находить максимумы.
Может просто прировнять производную этого выражения(или его квадрата) к нулю?
И так как косинус равен 0 только при \frac{\pi}{2} + n\pi
Можно перебирать х и у пока само значение косинуса не станет 0 и чтобы эти значения не выходили за рамки.
Я правильно вас понял?

[Sammael (Илья)]

Если вам надо перебирать значения, чтобы найти максимумы синуса, то возьмите паузу от химии и потратьте пару недель/месяц, на изучение математики. Вы должны чувствовать математику, чтобы не вязнуть в этом

[Sanjaster (Калиакбар Санжар)]

Кажется я понял, я посидел и увидел, что квадрат синуса это тот же синус, только без отрицательных значений, другими словами :

Вот тут, они просто отрицательные значения подняли вверх к положительным, и получили все максимумы.
Из за того, что ящик двухмерный(хотя выглядит трёхмерным), с одной стороны мы видим один максимум(я о фото выше), а с другой уже 2, для функций \phi_{2,1}, количество максимумов ведь зависит лишь от значения n, и если вглядываться вообщем, то максимумов 2.
Вообще, если так посмотреть, то чтобы найти количество максимумов нужно лишь n_x умножить на n_y

Для 4 пункта все так и работает:

С одной стороны это одномерный ящик с n = 1, и следовательно с 1 максимумом, с другой стороны это одномерный ящик с n = 4, и следовательно с 4 максимумами, а если перемножить эти значения и посмотреть на картину вообщем, то видим 4 максимума, также и для \phi_{2,2}
Я правильно рассуждаю?

Только я не понимаю как именно n влияет на количество максимумов, может оно уменьшает все значения х на n, и поэтому количество пиков увеличивается?
Имею ввиду, при sin(x), где 0<=х<=360
Есть 3 узла, при x=0,180,360
При sin(2x), есть 5 узлов, при х=0,90,180,270,360
А ну да, то чего достиг sin(x) вообщем, sin(2x) достиг уже к середине.
Но вот при просто sin(x) ведь должно быть 2 узла, а при sin(2x) 3 узла, как в книге:

А тут у нас 3 и 5 узлов, почему так?

[Sammael (Илья)]

Я не смогу ответить на ваши вопросы так, чтобы вы поняли, т.к. вы слишком увязли, хотя и некоторые вещи поняли (что двумерный ящик перемножение одномерных).

Вы увязли т.к. например не знаете школьную формулу
\sin(x)^2=\frac{1-cos(2x)}{2}
И по вашей фразе “двумерный ящик выглядит трехмерным” я понял, что концепции графиков функций вы не освоили на нужном уровне. И тригонометрию знаете лишь на уровне девятого, а необходим уровень выпускного класса.

Послушайте, я потратил тысячи часов на изучение математики в чистом виде, чтобы кванты понимать и решать на сборах и межнаре. Вы пытаетесь проскочить необходимое.

[Sanjaster (Калиакбар Санжар)]

@Sammael

Вы увязли т.к. например не знаете школьную формулу

Я ее знаю, но как ее использовать тут? Мне казалось я понял пункт 4, единственное не понимаю почему количество узлов в функций sin(x) = 3, а в точно такой же sin(\frac{\pi x}{L}) где \pi и L константы, и вроде не влияют на количество узлов, уже 2, как на фото выше

[Anton (Anton Morgunov)]

@Sanjaster

Я ее знаю, но как ее использовать тут?

Вот поэтому Илья и говорит, что вы не чувствуете математику. Если бы чувствовали – понимали бы как использовать.

@Sanjaster

Только я не понимаю как именно nnn влияет на количество максимумов, может оно уменьшает все значения х на n, и поэтому количество пиков увеличивается?

@Sanjaster

А ну да, то чего достиг sin(x)sin(x)sin(x) вообщем, sin(2x)sin(2x)sin(2x) достиг уже к середине.
Но вот при просто sin(x) ведь должно быть 2 узла, а при sin(2x)sin(2x)sin(2x) 3 узла, как в книге:

Функция синуса в общем виде имеет следующий вид: y=a \sin (bx+c) + d. Чтобы работать с функциями надо понимать влияние каждого из параметров a,b,c,d. Как изменится если функция если d увеличится на единицу? А если уменьшится? А если тоже самое станет с b?

На уроках математики объясняется, например, что такое период функции. И какой из параметров связан с этим периодом. И вот из понимания периода, его длины и его формы можно ответить на вопрос сколько узлов у функции.

То, что вы написали в последних двух сообщениях – попытка осмыслить решение, попытка придумать объяснение. В сравнении с некоторыми другими вашими темами это уже прогресс, но в данном случае это немного переходит в категорию “подгона” и на самом деле совершенно не оправданно, ибо ничем из этого не нужно заниматься если изучить темы алгебры 10 и немного 11 класса. Подойдите к школьному учителю и попросите научить вас анализировать функции. Параболу, синус, косинус. Не надо ему показывать задачи или уравнения квантовой химии – поймите математику в общем случае.

[Sanjaster (Калиакбар Санжар)]

@Anton

Как изменится если функция если d увеличится на единицу? А если уменьшится? А если тоже самое станет с b?

Возможно это риторические вопросы, и не нужно на них отвечать, но для достоверности, d влияет на перемещение по оси y, т.е если увеличится на единицу, то функция поднимется на единицу вверх по оси y, а если уменьшится то опуститься, верно?
b скорее всего влияет на количество повторений вот этих вот горок, скорее всего это и называют периодами.

@Anton

И вот из понимания периода, его длины и его формы можно ответить на вопрос сколько узлов у функции.

Значит ответ на этот пункт по большей части кроется в периодах?

@Anton

Подойдите к школьному учителю и попросите научить вас анализировать функции. Параболу, синус, косинус.

Так он скорее всего отдыхает где-то, поэтому писать и беспокоить его лучше не стоит, наверное лучше видео посмотрю

[DrMrmld (Azamat Zhaksylykov)]

@Sanjaster

но для достоверности, d влияет на перемещение по оси y, т.е если увеличится на единицу, то функция поднимется на единицу вверх по оси y, а если уменьшится то опуститься, верно?
b скорее всего влияет на количество повторений вот этих вот горок, скорее всего это и называют периодами.

Я в свое время любил баловаться всякими Geogebra и рисовать разного рода графики, чтобы понять, как что влияет. Можете проверить себя с помощью таких программ. А потом можно попытаться найти причину, почему это так (или не так).

@Sanjaster

Значит ответ на этот пункт по большей части кроется в периодах?

Ответ на этот пункт кроется в знании того, как меняется вид волновой функции с изменением n_x и n_y. По своей сути, просто в знании математики.

@Sanjaster

лучше видео посмотрю

Лучше почитать книгу. В сотнях страниц учебника явно больше полезной информации, чем в 20 минутах ролика.

[Sanjaster (Калиакбар Санжар)]

@DrMrmld

В сотнях страниц учебника явно больше полезной информации, чем в 20 минутах ролика.

А если 40-50 видео по 20 минут?

[Anton (Anton Morgunov)]

@Sanjaster

Возможно это риторические вопросы, и не нужно на них отвечать

Это вопросы на которые вы должны уметь отвечать чтобы решать эту задачу. Это то, что изучается на уроках математики. Я это написал чтобы показать вам что вы не знаете.

@Sanjaster

если 40-50 видео по 20 минут?

Если хотите торговаться идите на базар. Тут на форуме другим занимаются.

[amirbek (Амирбек)]

@Sanjaster

b скорее всего влияет на количество повторений вот этих вот горок, скорее всего это и называют периодами.

Всё это есть в программе 8 класса, так что советую сперва устранить уже имеющиеся пробелы в математике, прежде чем переходить к более сложным темам.