Не понимаю, почему именно 1/8 от объема шара является неотрицательным значением. И какой юнит у радиуса шара? Если считать по юнитам, то получается, что у радиуса нет юнита.
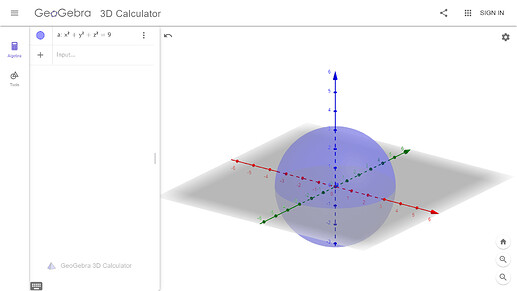
n_x^2+n_y^2+n_z^2 \le const — это шар. Если представить трехмерный график, то получится шар с центром в начале координат, у которого радиус равен \sqrt{const}. Благодаря координатам, шар делится на 8 равных частей. Только в одной из этих восьми частей все координаты имеют положительный знак. Поэтому \frac{1}{8}.
P. S. На рисунке сфера, потому что стоит знак равенства.
Теперь понятно почему 1/8 от объема это число состояний. Но почему число состояний определяется с помощью объема?
Представим, что у нас спросили не количество состояний, у которых энергия меньше указанной, а количество состояний с такой же энергией. Тогда нам надо было бы, чтобы n_x^2+n_y^2+n_z^2=const. Из-за того, что уровни могут быть вырожденными, у нас есть куча состояний, у которых энергия равна тому, чему нам надо. То есть, любая комбинация n_x^2, n_y^2 и n_z^2, которая удовлетворяет этому равенству, будет нашим решением. Это равенство дает сферу в трехмерном графике, что означает, что каждая точка на поверхности этой сферы является нашим решением. А как можно посчитать количество точек (aka решений)? — Вычислить площадь поверхности.
Но в данном случае ситуация немного другая, потому что нас еще интересуют те случаи, когда энергия ниже указанной. То есть нам надо для каждого меньшего значения энергии посчитать площадь поверхности сферы и просуммировать все результаты. А это по определению является объемом.
Либо можно сразу сказать, что n_x^2+n_y^2+n_z^2 \leq const это шар и каждая точка внутри этого шара является решением уравнения, а значит решением нашей задачи. А чтобы посчитать количество точек внутри шара, очевидно, надо просто найти его объем.
Может еще появиться ощущение, что мы забываем о том, что n — натуральное число, потому что мы просто ищем любые решения задачи (якобы необязательно целые). Но это не так, потому что возьми, например, состояние (1,1,1) и оно будет занимать ровно 1 кубическую единицу. (2,2,2) — 8 куб. ед. (8 состояний, в которых n \leq 2). Это из-за того, что у нас есть аксиома о том, что единичный куб имеет объем 1 куб. ед., по аналогии с тем, что единичный квадрат имеет площадь 1 кв. ед.
Я не понял объяснение про натуральное число. Если у нас есть шар с радиусом 2 единицы и условие, что n_{x}^2 + n_{y}^2 + n_{z}^2 < 2^{2} , где n - натуральное число, то число состояний равен одному (1, 1, 1) , а по формуле 4,18(6).
Дело в масштабе и величине значений. По сути да, объём 1/8 шара не идеально равен числу возможных состояний, однако для больших значений, таких как в задаче, это будет очень хорошим приближением, так как при больших значениях отличие между 1/8 объёма и реальным числом состояний становится очень незначительным, по сравнению с величиной полученного ответа.
Для маленьких же значений это приближение работает очень плохо, что показывает пример со значением радиуса 2.
Я бы это интерпретировал, сказав, что в это число вошли решения, где некоторые n принимают нулевое значение (которых как раз 3). Понятное дело, что саму поверхность сферы мы включать не должны, потому что неравенство строгое, но мы не можем выбрать наугад какой-нибудь рандомный радиус меньше 2, нам подходит даже тот, что бесконечно меньше чем 2. То есть решение частично не точное в основном из-за двух факторов:
- Мы “захватываем” некоторые решения, где некоторые n=0
- Мы засчитываем поверхность сферы, хотя в условии говорится о “строго меньше” (не “меньше или равно”)
По хорошему надо бы эти значения отдельно считать и отнимать от числа, которое давалось в решении, но с увеличением радиуса вклад этих решений все менее и менее значителен.
А тот хвостик, который ты получил после запятой связан с тем, что эти точки не полностью заполняют шар. Из каждой точки можно сделать куб, проведя прямые, перпендикулярные трем плоскостям. Но шар, который тебе нужен, будет всегда чуть больше чем кучка таких кубиков.