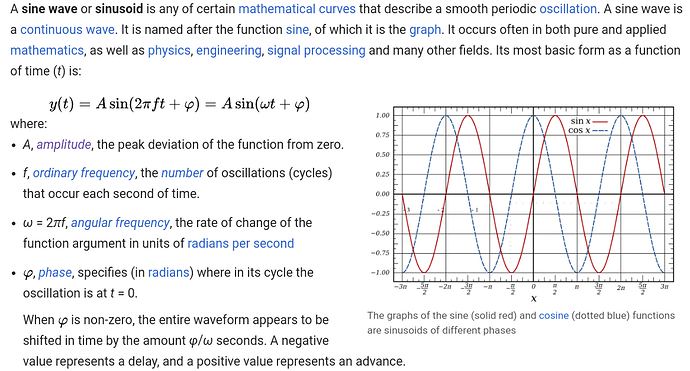
Я не понял, что именно описывает волновая функция. Длину амплитуды после t секунд и x метра?
В викпедии написано, что А - амплитуда. То есть мы берём длину амплитуды чтобы найти длину амплитуды? Не понятно
1 лайк
x - measured along the direction of propogation. То есть x это расстояние между начальной и конечной точки волны, как бы “измерятеся вдоль вектора распространения”.
t - просто момент времени
2 лайка
Чуть подробнее:
Мы знаем, что если волна распространяется вдоль одной оси, то её скорость выражается как производная от координаты: v=dx/dt. Если проинтегрировать, то получается vt-x=const. Это означает то, что если уравнение волны описывается некоторым выражением f(x,t), то именно при комбинации f(vt-x) или f(t-x/v) значение функции будет сохраняться при определённой паре значений (x,t). В случае с синусоидальной волной это обретает привычную форму A\cos (\omega t - \omega x/v), или, в общем случае с тремя координатами и использованием волнового вектора k=\omega /v мы получаем
f(x,t) = A \cos (\omega t - \vec{k} \cdot \vec r)
причём скалярное произведение раскрывается как \vec k \cdot \vec {r} = k_x x + k_y y + k_z z
6 лайков
Спасибо за объяснение формулы. Но хотелось бы узнать что дает значение волновой функции. Скажем значение всех variable даны и у меня вышло 3,5. Что это означает? Длину амплитуды?
2 лайка
Зависит от того, что описывает синусоида. Если это уравнение напряжённости электрического/магнитного поля у волны, то 3.5 это значение напряжённости в данный момент времени. В этом вопросе это просто даёт значение волновой функции.
1 лайк
В моем случае волновая функция описывает амплитуду. Единственное, что амплитуда имеет это длина. Значит оно описывает длину амплитуды? Тогда откуда взять значение А, которая тоже является амплитудой? Взять наибольшую амплитуду? Наименьшую?
1 лайк
Амплитуда тут является постоянной величиной ( по всей видимости). Функция синуса принимает значение от -1 до 1, и умножая её на А, мы получаем какую-то величину в пределах от -А до А, что является мгновенным значением волновой функции
3 лайка
хотя касательно задачи пусть химики ответят)
2 лайка
У самой волновой функции нет физического смысла. Но если волновая функция нормирована, то \Psi(x) \cdot \Psi^*(x) дает плотность вероятности. Можно привести аналогию с обычной плотностью (массы): если у нас есть зависимость \rho(V), то площадь под графиком этой зависимости — \displaystyle\int\limits_{a}^{b} \rho(V) \text{d}V — дает массу. Если взять конкретное значение t, можно будет рассмотреть (нормированную) функцию \Psi(x) и площадь под ее графиком — \displaystyle\int\limits_{a}^{b} \Psi(x) \cdot \Psi^*(x) \text{d}x — даст уже вероятность нахождения частицы в отрезке x \in [a,b]. Зависимость от времени, как я понял, дает то, что вероятность нахождения частицы в каком-то отрезке меняется со временем.
Еще могут быть два интересных частных случая: когда отрезок — вся прямая (если рассматриваем зависимость от x,y,z, то все пространство) и когда это всего одна точка. В первом случае вероятность равна 1, потому что это вероятность нахождения частицы где-нибудь. Во втором случае, вероятность равна нулю, потому что всех точек бесконечно много. Интересен этот случай тем, что казалось бы вероятность равна нулю, но событие ведь может случиться. И про это есть хорошее видео — https://youtu.be/2xdferBi2yM. Просто хотел поделиться 
.
10 лайков
Я так понял автор запутался ибо считает что \Psi(x,t) и x измеряют некую длину.
Начнем с обычной синусоидной волны (то, что указано в вики). Что такое y(t)? У нас есть некая переменная (для простоты – считайте физическая величина), чье значение не постоянно во времени. В некоторых случаях, для некоторых переменных, можно применить модель синусоидой волны и сказать, что эта величина имеет значение y(t). Т.е. y(t) дает нам понять значение определенной величины в любой момент времени. Поскольку область значений синуса ограничена [-1;1], амплитуда показывает максимально (и минимально) возможное значение величины.
Волновая функция в квантовой механике - функция нескольких переменных. Помимо времени, в простейшем случае добавляется координата x. Т.е. мы имеем функцию y(x,t), которую обозначим как \Psi(x,t).
Что такое функция от двух переменных: пространства и времени? Это функция, которая помогает узнать чему равно значение той или иной величины в определенный момент времени и в определенной точке пространства. Что определяет функция? Что угодно. В данном случае, строго говоря, сама волновая функция не имеет физического смысла. Но вот если эту функцию дифференцировать, умножать, интегрировать – можно получать энергии, вероятности и прочую радость.
Иными словами, ключевое - понять, что амплитуда – не физическая высота физической волны. Это просто множитель функции, описывающий значение определенной величины, которая изменяется в пространстве и времени как синусоидная волна.
5 лайков