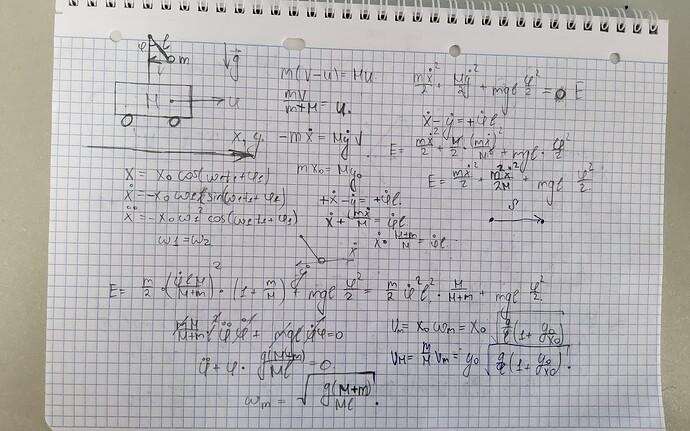3.1.15. Амплитуда малых колебаний математического маятника, стоящего
на тележке, равна хо, а амплитуда колебаний тележки уо. Длина нити маятника l.Определите максимальную скорость маятника и тележки. Трением пренебречь.
не пойму почему не выходит,может ли здесь быть опечатка?
у меня сошлось, ты правда жёстко усложнил. Там просто ЗСИ и ЗСЭ записать, типа.
\frac{mg(x_0+y_0)^2}{2l} = \frac{mv_1^2}{2} + \frac{Mv_2^2}{2}
mv_1 = Mv_2
mx_0=My_0
решим верхнее уравнение относительно v_1
v_1=\sqrt{\frac{Mg}{(M+m)l}(x_0+y_0)^2}=\sqrt{\frac{x_0g}{(x_0+y_0)l} (x_0+y_0)^2}=x_0 \sqrt{\frac{g}{l} (1 + \frac{y_0}{x_0})}
решим верхнее уравнение относительно v_2
v_2=\sqrt{\frac{mg}{(M+m)l}(x_0+y_0)^2}=\sqrt{\frac{y_0g}{(x_0+y_0)l} (x_0+y_0)^2}=y_0 \sqrt{\frac{g}{l} (1 + \frac{x_0}{y_0})}
И выходит ответ как в Савченко. Где ошибка у тебя не знаю, у тебя очень не упорядоченное решение(ну либо я дурачок)
я не дома сейчас,отвечу позже .А так я реально эту задачу беспорядочно решил на листке)
Здравствуйте , а откуда появились уравнения mV1=MV2 и mx0=My0
Закон сохранения импульса по оси 0X, ну и условие того что центр масс по оси 0X не подвижен, это следует из того что по 0Х внешних сил нет
спасибо , ещё не очень понимаю почему в левой части зсэ где m×g((x0+y0)^2)/2l там только масса маятника , я так понял что это энергия колебаний и думал что раз колеблятся оба тела там должна быть суммма масс m+M , наверное я не прав, можете ли пожайлуста объяснить?
Это потенциальная энергия, короче там нужно рассмотреть максимальное отклонение маятника от положения равновесия, и выразить изменение высоты через отклонение, я щас не могу расписать, попробуйте сами. И там не должно быть суммы масс так как тележка не поднимается при движении.
Да получилось , спасибо большое за пояснение