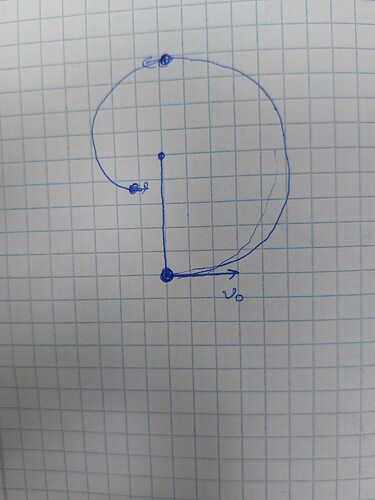
Математическому маятнику с гибкой нерастяжимой нитью длины l сообщают в начальный момент горизонтальную скорость v_0. Определить максимальную высоту его подъема h, как маятника, если \sqrt{5lg} > v_0 > \sqrt{2lg}. По какой траектории будет двигаться шарик маятника после того, как он достиг максимальной высоты h на окружности? Определить максимальную высоту H,достигаемую при этом движении шарика.
Помогите с решением этой задачи
Рисунок будет такой?
Из условия v_0<\sqrt{5gl}, нить будет иметь нулевое натяжение до достижения шарика верхней точки.
Можно записать:
T=0
m\frac{v^2}{l}=mg\sin{\alpha} , где альфа - угол между нитью и горизонталью в момент, когда она ослабнет.
Также закон сохранения энергии:
m\frac{v^2}{2}+mgl(1+\sin{\alpha})=m\frac{v_0^2}{2}
Отсюда найдется максимальная высота, а траектория будет параболой, потому что сила натяжения будет нулевой и шарик будет лететь так, как если бы его бросили под углом к горизонту
3 лайка