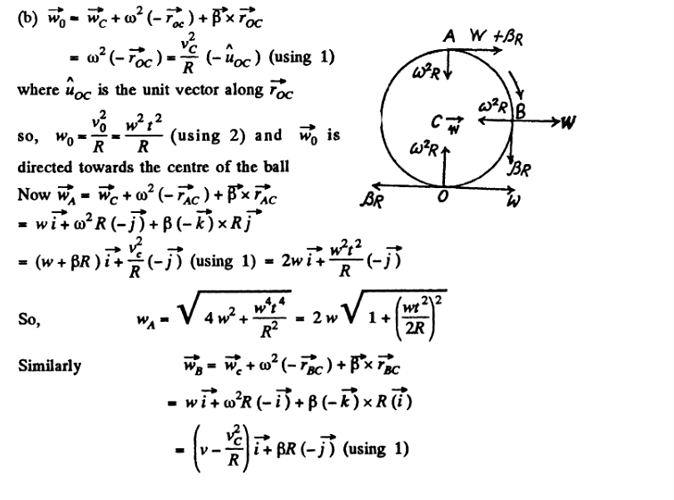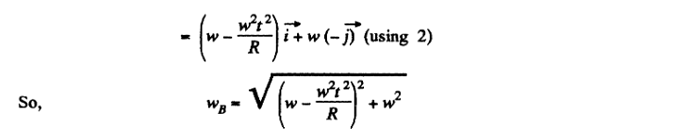Объясните, если не сложно, решение Сингха, а то я вообще понять его не могу, заранее спасибо! Вопрос (a) я сам решил и (b) вроде тоже начал, но вот при нахождении ускорении (.)А у меня с решением ответы расходятся, и я не понимаю почему)
Вот мое решение:
у тебя проблема в понимании самой задачи: внимательно распиши компоненты ускорений в данной точке и посмотри, как они складываются
Соглашусь с замечанием Алишера. Ответ найти можно абсолютно случайным образом и конечно же оно может быть правильным, но понимание самой задачи будет иметь другой смысл в своей голове. попробуй нарисовать рисунок движения шара со всеми проекциями ускорения. Посмотрим на этот рисунок от Синха:
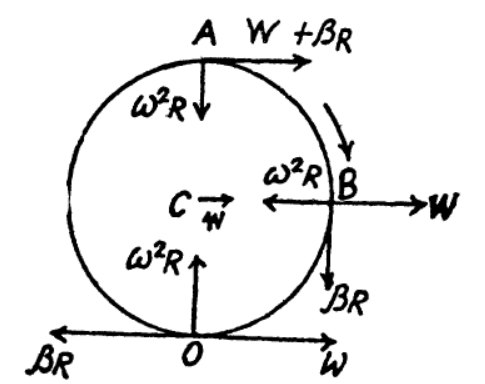
Тут для каждой точки грамотно было расписано определенное направление и для каждого из них действовало три ускорения: тангенциальное, центростремительная и ускорение самого шара. Возьмем например точку О и запишем все в векторном ввиде:
В точке О тангенциальное ускорение и данному ускорение точке от центра обода направлены противоположно и они автоматически вычитываются. Думаю, это тебе было доказано еще в этой задаче.
Получается ускорение в нижней точки равна центростремительному ускорению. Да, это совпадает с твоим ответом, но очень важно понять почему так случилось, ведь например если написанно чуть выше не было доказано, были трудности с другими влиятельными ускорениями.
Дальше возьмем точку А, дальше пишем точно такую же векторную формулу и видим по рисунку, что трюк с точкой О уже не сработает. Только самое приятное, что эти ускорения равны друг другу(также было доказано в задаче 1.52, которую ты наверняка решил) и соонаправлены, значит у них получится более приятная векторная форма ускорения точки:
Дальше все видим, что эти вектора перпендикулярны, очевидно, что нужно использовать теорему Пифагора.
Думаю двумя примерами ты сможешь найти и ускорение В.
Важное упоминание:
Я конечно, понимаю, что могу быть не прав, но мне кажется уже и в физике люди начинают неправильно задавать вопросы. Проблема, конечно не в частоте задаваемых вопросов одного задачнике, а вклад своего внимания в одну задачу. Если что-то не понимаешь попробуй откопать решение в интернете или что - то еще связанное с ним, как то расширить мыслительный процесс, которому ты и другие способны. Да, я конечно видел твои неплохие попытки решения задач, но когда думаешь, что - то не удается попробуй хоть как - то попробовать решить, нарисовать рисунок, поставить цифры и посмотреть на поведение с уравнения, потом сопоставить с вариантом Синха. Многое было также упомнено в самом книге Иродова.
Решая 5 задач в день, если ты хорошо стараешься вникнуть в них - это неплохо, только для них нужен правильный порядок решения задач, которые я указал выше. При правильном подходе ты сможешь позже сможешь нарастить темп.
Написав это я не имел ввиду, что “все, больше 1 вопроса в неделю запрещено”, конечно этот форум рад помочь олимпиадником с трудностями. Но нужно улучшать и свои навыки в понимании задач тоже. Не вникнув в задачу - это будет тратой сил и времени.
Ну. В заключении скажу, удачи и правильно следуй порядку решения задач!
Вот сейчас разбираюсь с этим решением и параллельно смотрю на решение Синха, вот не могу понять почему он там взял Roc с минусом, у него там: a0=ac+β×R+ω^2(-R)
ну смотри, как думаешь, что с чем связаны вектора \vec{i} и \vec{j}
i с ox, а j с oy
Я же правильно понимаю, что это орты координат?
Да, теперь взгляни на рисунок и ты видишь, что центростремительное ускорение направлено противоположно условно по глазу противоположно оси Х. Значит его орта тоже будет отрицательной. Если так расписать, то так \vec{R}=R\vec{(-i)}
А разве в точке O центростремительное уск-е не перпендикулярно ox?
Аа я думал ты имел ввиду про ускорение в точке В
По моему там ошибка, потому что в след пункте в нахождении ускорения в точке А, там вектор указали правильно.
Понятно, спасибо!
