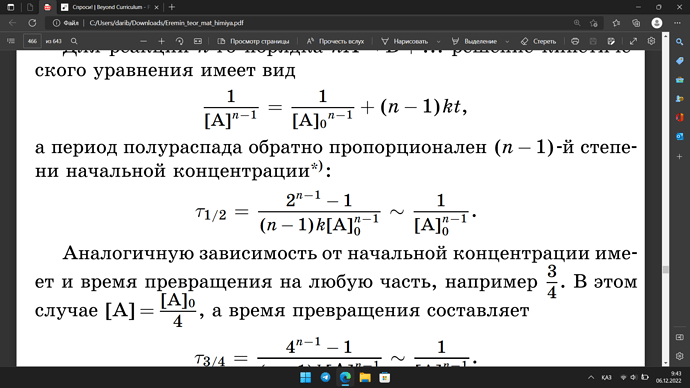
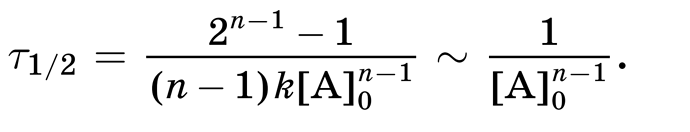почему в формуле нахождения полураспада реакций n-го порядка, мы пренебрегаем
(n-1) \cdot k, а еще в книге показано, что это уравнение верно для реакций
\ce{nA -> D + ...}
если у нас в реагентах будет больше одного вещества, то там мы используем, такую же формулу или эта уже будет неправильной ? в двух случаях
А) если те исходные вещества будут иметь одинаковую концентрацию
Б) если у исходных реагентов будут разные концентраций
А еще в этой главе показали формулу только когда $[A]=[B]$а если у нас они будут не равными, то какая формула, и эта формула распространяется на на другие порядки кроме второго ?
а где пренебрегли?
Если концентрации исходных веществ равны и общая сумма порядков равна n, то можно использовать эту формулу. Но лучше самостоятельно выводить для каждого случая.
Это случай посложнее, если вы учите это для Олимпиадной химии, то решения такого относительно сложного интеграла у вас не попросят.
1 лайк
вот в этой формуле, они оставили только \displaystyle \frac{1}{[A]^{n-1}_0}, я не смог вывести как тут все сокращается можете показать ?
Была задача на вывод этой формулы на республиканской олимпиада 2020 года. В общем то там формула посложнее и для решения интеграла нужно использовать метод неопределенных коэффициентов.
Мне кажется вам нужно ознакомиться с выводами формул. Порядок реакции это не просто термин, а степень концентрации какого то вещества. Вот эту степень нужно учитывать во время интегрирования, а соответственно степень влияет на результат. Покажу на примере второго порядка:
-\frac{dA}{dt}=k[A]^2
-\frac{dA}{[A]^2} = k dt
\int_{A_0}^A \frac{dA}{A^2} = -k \int_0^t dt
Дальше пользуясь основными формулами интеграла можете вывести полное уравнение скорости.
P.S тут везде должно быть [A], я иногда забывала писать
6 лайков
знак ~ означает прямо пропорционален, а не равно. Здесь говорится, что время полураспада прямо пропорционален 1/[A]0n-1, а значит обратно пропорционален [A]0n-1.
5 лайков
Мой мат аппарат это матеша 9го класса…
Думаю для этого сначала нужно поднять свой мат аппарат до знания интеграллов/производных.
еее, я думал, что это примерно равно.
1 лайк
тут кстати строго говоря дается формула для A+B+... \rightarrow D, потому что для реакции nA \rightarrow D скорость определяется как
\frac{1}{n} \frac{d A}{dt}
за счет чего перед (n-1)k появится еще один фактор n, т.е. n(n-1)k. Иногда этот n суют в k (переопределяя k'=kn), тогда формула как бы одинаковая для всех случаев.
Это все верно
для этого случая.
а тут нет, тут надо интегрировать каждый отдельный случай.
Что-то я тут поплыл 
Вернемся к этому разговору когда научитесь интегрировать хотя бы y'=y^n для n=0,1,2.
договорились