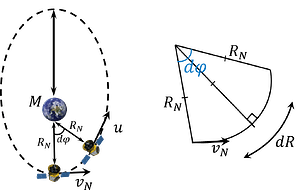Плоскость орбиты спутника разбита на секторы с общей вершиной в центре планеты массы M и одинаковыми малыми углами раствора dϕ.
Найдите изменение скорости спутника при прохождении каждого сектора, если
его скорость в перицентре vп, а расстояние от спутника до центра планеты в
перицентре rп.
1 лайк
Второй закон Кеплера гласит, что скорость заметания секторной площади постоянна, т.е.
\frac{dS}{dt}=const
Нам известны расстояние спутника r_п в перицентре и его скорость v_п в этой точке. В перицентре за малый промежуток dt заметается очень малый сектор, который можно считать равнобедренным треугольником с длиной бедра r_п и основанием v_п dt. Значит в этой точке dS_п=\frac{1}{2}v_пdt \cdot r_п, либо
\frac{dS}{dt}=\frac{v_пr_п}{2}.
Теперь перейдём к вопросу об изменении скорости при каждом прохождении угла d\varphi. Если в данный момент расстояние между спутником и планетой равно r, то
dS=\frac{1}{2}r^2 d\varphi.
Второй закон Ньютона записывается в таком виде:
\frac{dv_r}{dt}=\frac{GM}{r^2}=\frac{GM}{v_п r_п}\frac{d\varphi}{dt},
причём индекс r означает изменение радиальной компоненты скорости в направлении к центру планеты. Отсюда получаем окончательный ответ:
dv=\frac{GM}{v_п r_п}d\varphi.
8 лайков
В течение короткого времени, dt, тело движется по дуге окружности d\varphi с радиусом-кривизной траектории R_n.
Второй закон Ньютона для внешней силы – силы тяготения
ma=\frac{GmM}{R_n^2}
По определению ускорения
a=\frac{dv}{dt}\Rightarrow \frac{dv}{dt}=\frac{GM}{R_n^2}\quad (1)
За небольшой промежуток времени dt
dR=v_ndt\quad (2)
По определению длины дуги окружности, соответствующая углу d\varphi
dR=d\varphi \cdot R_n\quad (3)
Подставляем (2) и (3) в (1)
\frac{dv}{dR}v_n=\frac{GM}{R_n^2}\Rightarrow \frac{dv}{d\varphi}v_n=\frac{GM}{R_n}
После преобразования мы можем получить изменение скорости спутника
\boxed{dv=\frac{GM\cdot d\varphi}{R_nv_n}}
Источник: savchenkosolutions.com
4 лайка