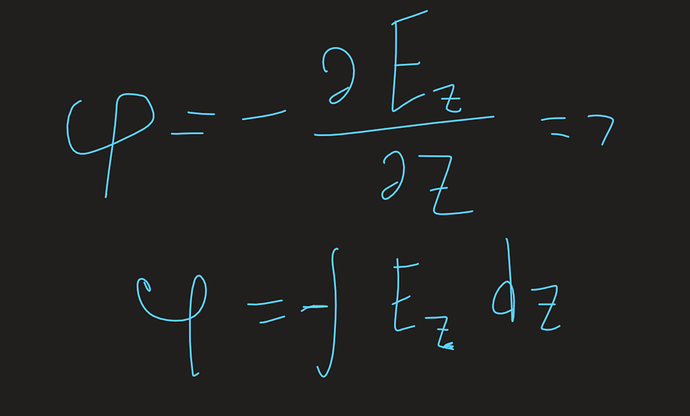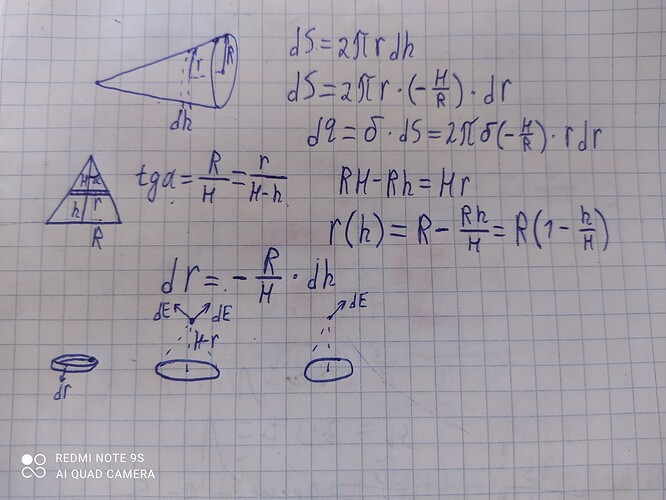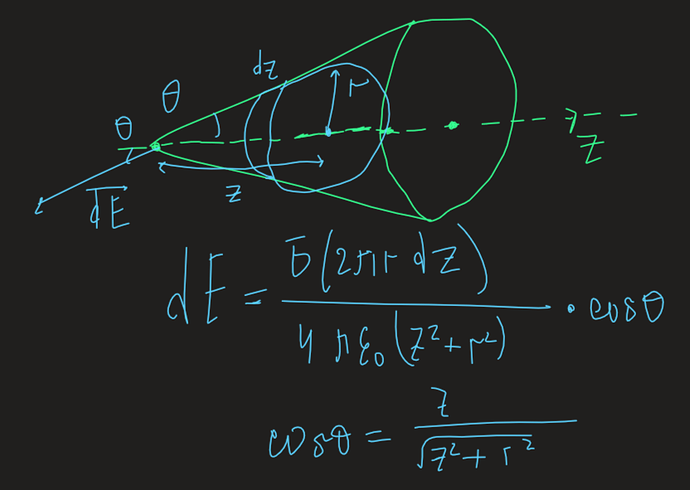2 лайка
Есть попытки решения?
2 лайка
Если что там тоже самое как в том примере с кольцом, но ты предполагаешь, что конус имеет высоту h и разделяя конус на малые элементы - кольцы с толщинами dz находишь напряженность интегрированием.
Воспользовавшись этой формулой можно найти потенциал
5 лайков
Я вот так начинал решать.Проблема в том что dq это заряд полного кольца.Теперь нужно разделить на маленькие точки?
1 лайк
Нужно dS по-другому написать. То есть dS=2\pi r dh правильно, затем можно dh и r написать через угол \alpha, который ось образует с образующей конуса. И получим dq, который нам нужен.
3 лайка
dq=2πrdzŏ
Это же заряд кольца?
Разве можно напряженность так написать?
Можно, напряженность ведь \frac{kq}{r^{2}}