(Речь идет про силу оказываемую на связанные заряды диэлектрика между пластинами заряженного конденсатора)
Не могу понять смысл интеграла, почему мы берем dE?Можно это как то по другому объяснить, впервые сталкиваюсь с таким случаем
1 лайк
Скинь условие задачи
1 лайк
2.151. Плоский конденсатор, расстояние между пластинам которого d=1,0 мм, опустили в горизонтальном положении в воду, которая целиком заполнила его. Затем конденсатор подключили к постоянному напряжению U = 500 В. Найти приращение давления воды в конденсаторе.
1 лайк
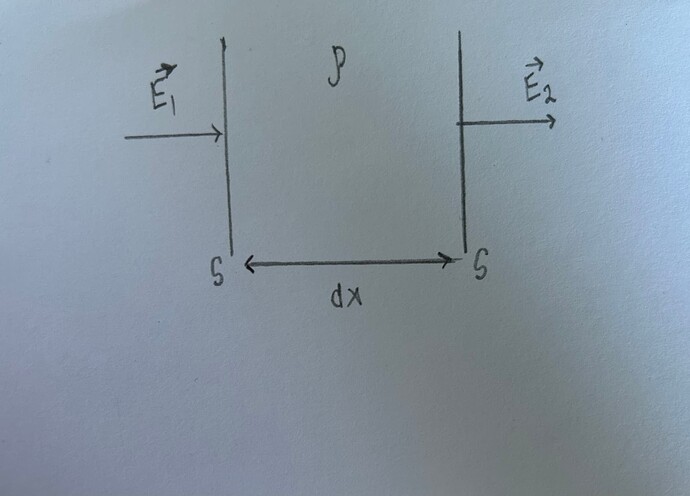
Так, начнем с того что сила действующая на точечный заряд при присутствии внешнего электрического поля равна \vec F=q\vec E, получается для непрерывного распределения заряда сила будет d\vec F=dq\vec E. Чтобы найти полную силу мы должны естественно проинтегрировать F=\int dqE. Так как заряды распределены по поверхности конденсатора, то dq=\sigma dS, получается сила F=\int\sigma EdS. Теперь рассмотрим общий случай произвольного слоя заряда, причем возьмем такой слой заряда, что его толщина равна dx, а площади граничных поверхностей фиксированы и равны S. Так как у нас появляется толщина слоя, то у нас появляется и объем, значит заряды распределяются не по поверхности, а по объему. Когда мы считали, что слой заряда бесконечно мал и заряды попросту распределяются по поверхности мы делали аппроксимацию, т.к. в реальности толщина присутствует и равна dx, присутствует также и объемная плотность зарядов \rho
Применим теорему Гаусса для этого слоя, причем мы должны использовать дифференциальную форму теоремы Гаусса
\nabla \cdot \vec E=\frac{\rho }{\varepsilon_0}\rightarrow E(x+dx)-E(x)=\frac{\rho dx}{\varepsilon_0}=E_2-E_1
Очевидно, что E_2-E_1=\frac{\sigma}{\varepsilon_0}, значит поверхностную плотность \sigma можно заменить \rho dx. Учитывая то, что площадь имеет фиксированное значение выражение для силы становится dF=ES\rho dx, запишем разницу E_2-E_1=E(x+dx)-E(x)=dE и \rho dx=\varepsilon_0 dE сила
dF=\varepsilon_0SEdE\rightarrow F=\int\limits_{E_1}^{E_2}\varepsilon_0SEdE=\frac{\varepsilon_0S}{2}(E_2^2-E_1^2)
Силу также можно записать как
\varepsilon_0(E_2-E_1)=\sigma\rightarrow F=\frac{\sigma S}{2}(E_1+E_2)
Так как толщина слоя бесконечно мала, то заряд распределенный по этому слою с хорошим приближением можно считать q=\sigma S. И конечное выражение для силы выглядит как F=\frac{q(E_1+E_2)}{2}=q\langle E\rangle =qE_{aver.}. Внутри конденсатора поле присутствует только между пластинами конденсатора и снаружи оно равно нулю, поэтому сила F=\frac{qE}{2}. Здесь один из полей E_1 и E_2 берем равным нулю, а другой берем как E- внутри конденсатора. Отсюда и появляется коэффициент \frac{1}{2}.
11 лайков
Нет ты не можешь рассматривать связанные заряды, распределенные по объему как два заряда. Если у нас связанные заряды распределены по объему, то их плотность соответственно \rho_b=-\nabla\cdot \vec P, если по поверхности, то \sigma_b=\vec P\cdot \hat n.
Нужно различать свободные и связанные заряды. То что ты говоришь это все равно что если поставить какой-то заряд во внешнее поле то мы должны учитывать силу с которой она действует на самого себя. Но сила действующая заряд равна \vec F=q\vec E_{внеш.}, поэтому сила, действующая на связанные заряды равна \vec F_{связ.}=\int dq_{связ.}\vec E_{своб.}, то есть здесь поле берешь со стороны свободных зарядов. И вообще если ты знаешь природу связанных зарядов, то ты должен знать что это большое количество диполей, которых ты рассматриваешь как заряды. Поляризованные заряды создают свое собственное поле \vec P. И сила действующая на диполь \vec F=(\vec p\nabla )\vec E_{ext.}, то есть сила действующая на поляризованные заряды зависит только от внешнего поля \vec E_{ext.} и поле самих поляризованных зарядов \vec P здесь никак не причастно. В данном случае внешнее поле для связанных зарядов это поле свободных зарядов.
10 лайков
а всё таки, почему связанные заряды между собой не взаимодействуют? я не очень понимаю причину
1 лайк
Мне кажется эту задачу легче решить так, во первых ты разделяешь конденсатор на слой воды и воздух, потом ищешь силу через энергию, после пишешь что слой воздуха стремиться к нулю а слой воды к 1 мм. И у тебя выйдет ответ.
5 лайков
Когда мы рассматриваем систему из связанных зарядов, то силы взаимодействия между ними это внутренние силы и их векторная сумма равна нулю: \vec F_{ij}=-\vec F_{ji}\rightarrow \sum_{i,j} \vec F_{ij}=0.
1 лайк
Взаимодействуют, ещё как вщаимодействуют, мы внешним полем скорее их идиллию нарушаем. Вопрос скорее в сторону химии. Как у вас с химией?
5 лайков
Ну это понятно, мой вопрос скорее в сторону того почему давления дополнительного они не создают?(я не понял что вы писали 2 месяца назад). Короче такой че вопрос как у @Upward, но я не понял почему мы не учитываем это
Вот есть у нас сила со стороны 1 пластинки связанных зарядов, она притягивает к себе другую пластинку, и наверное делает вклад в давление, и так же со второй.
Может быть я просто не умею считать давление, но объясните ещё раз, пожалуйста
Не выше школьного уровня