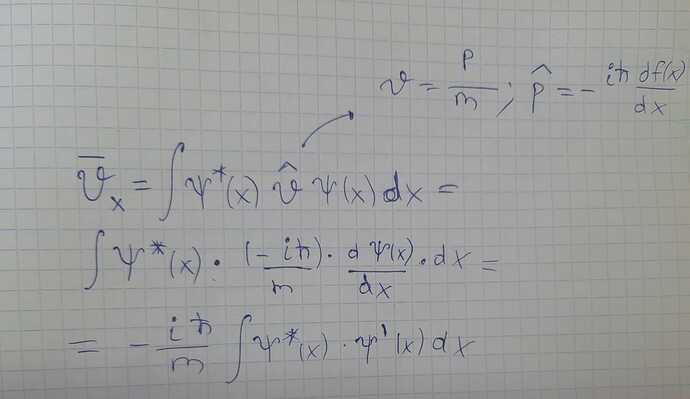Как продолжить вывод и привести это к виду без знака комплексно-сопряженной пары?
И вообще, побьют ли меня на районе математики за такое обращение с операторами? Можно ли в формуле v=p/m заменить v и р на соответствующие операторы или это делается как-то по другому?
1 лайк
А у вас комплексная функция? Или она чисто действительная?
1 лайк
Волновая функция ведь вполне себе может быть комплексной, разве нет? (Мы ж поэтому берем квадрат модуля, чтобы минус не получился) (П.С. задача про электрон в двухмерном ящике Lx, Ly). Ну да согласен, если комплексная часть iy равна нулю, то просто ψ*=ψ, где
ψ=x+iy
ψ*=x-iy
Аааа я понял, надо сперва поменять оператор на “собственное значение” и тогда уже можно будет использовать формулу v=p/m, да?
1 лайк
С одной стороны у тебя стационарные волновые функции.
Их всегда можно в действительном виде брать если есть желание.
С другой стороны у тебя оператор скорости эрмитов, т.е. ты можешь красиво это все превратить в другое выражение, но нужен некий навык.
С третьей стороны можно по частям бахнуть твое выражение и там гамильтониан можно будет достать и ещё интереснее сделать, но это ещё чуть больше требует навыка.
2 лайка
То есть если ограничиться на этом, то впринципе можно как я выводить нужные формулы, да?
А как понять, самосопряжен ли оператор самому себе или нет?
Это не ко мне, я Tomas calculus бросил после главы с производными)))))
1 лайк
Интегрирование по частям
Никак, в этом примере с самого начала допускается, что волновая функция действительная
2 лайка
А нельзя заменой переменной? dѱ/dx×dx=dѱ, дальше решаем процтецкий интеграл ѱdѱ
1 лайк
ну или так)
2 лайка
Ну если ты знаешь, что у тебя стационарные решения, то да.
Проверить в лоб можно. Но вообще все операторы у наблюдаемых классических, они эрмитовы.
Я имел ввиду вот такое.
Из-за эрмитовости:
\overline v_x=\int \psi^* \hat v \psi\,dx =\int \psi \hat v \psi^*\,dx=-\frac{i\hbar}{m}\int \psi^* \psi'\,dx =-\frac{i\hbar}{m}\int \psi\psi'^*\,dx
Значит
\overline v_x=1/2\cdot \left( \int \psi^* \hat v \psi\,dx +\int \psi \hat v \psi^*\,dx \right)=-\frac{i\hbar}{2m}\int \left( \psi^* \psi'+ \psi'^* \psi \right) \,dx
Ну и тут уже видно, что это сворачивается в производную от квадрата модуля плотности вероятности и ответ как у них.
Ну или вообще вот так, прокрутив взятие по частям в обратную сторону:
\begin{gathered}
\overline v_x=\int \psi^* \hat v \psi\,dx =-\frac{i\hbar}{m}\int \psi^* \psi'\,dx =-\frac{i\hbar}{m}\int \psi^* \,d \psi=\\
\underbrace{
-\frac{i\hbar}{m} (\psi^*\psi) \Biggl|_{- \infty}^{+ \infty}}_{\substack{\text{просто ноль, ибо }\\ \text{на бесконечности}\\ |\psi|^2 \text{ обращается в 0 }}
}
+\frac{i\hbar}{m} \int \psi'^*\psi \,d x=\frac{i\hbar}{m} \int \psi'^*\psi \,d x
\end{gathered}
Тут можно сравнить последнее выражение в первой формуле из моего сообщения, и последнее выше и получается просто
\overline v_x=-\overline v_x
Что как бы тоже дает сразу ноль для средней скорости
3 лайка