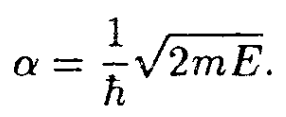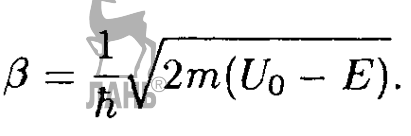Здравствуйте форумчане! У меня проблема с элементом, окруженным красным карандашом. Когда мы берем квадрат модуля, то данная экспонента куда то пропадает, а куда и почему я не знаю. Если что, это Савельев, 5-ый том, пятое издание.
Что такое модуль и квадрат модуля комплексного числа вы знаете?
1 лайк
Здравствуйте!
Покажу пример,
Запишем комплексное число z в показательной форме: z = r e^{if},где r - модуль числа, f - его аргумент.
Комплексное сопряжение: z^* = re^{-if} (меняем знак у мнимой единицы в показателе)
Модуль комплексного числа: |z| = \sqrt{z \cdot z^*} = \sqrt{re^{if} \cdot re^{-if}} = \sqrt{r^2 \cdot e^0} = r ( экспоненты сокращаются)
Тепепь рассмотрим наш пример:
У вас есть выражение для a_3:
a_3 \approx -\dfrac{(4ni \cdot \exp(-i \alpha l))}{(n - i)^2} \cdot \exp(- \beta l)
Когда вы берете квадрат модуля |a_3|^2,вы должны умножить a_3 на его комплексное сопряжение a_3^*:
a_3^* \approx - \dfrac{(4ni \cdot \exp(i \alpha l))}{(n + i)^2}
Теперь перемножим a_3 и a_3^*:
|a_3|^2 = a_3 \cdot a_3^* \approx \left[ \dfrac{(4ni \cdot \exp(-i \alpha l))}{ (n-i)^2} \cdot \exp(- \beta l)\right] \cdot \left[ \dfrac{(4ni \cdot \exp(i \alpha l))}{ (n+ i)^2} \cdot \exp(- \beta l)\right]
При перемножении экспоненты с противоположными знаками в показателе ( \exp(-i \alpha l) и \exp(i \alpha l)) дают единицу ( \exp(0) = 1). Экспоненты с - \beta l просто перемножаются, давая \exp(-2 \beta l)
В результате остается:
|a_3|^2 \approx \dfrac{ 16 n^2 }{(n^2 + 1)^2} \cdot \exp(- 2 \beta l)
Надеюсь я смогла помочь, если будут ещё вопросы задавайте, постараюсь ответить 
3 лайка
Кстати когда пишете функцию экспоненты, пожете написать через черточку, и она станет прямой:
$\exp(x)$
дает \exp(x)
И чтобы писать большие скобки в которых вмещаются дроби (и вообще все что угодно), используйте команды \left и \right. Например
$$
\left(\dfrac{\dfrac{1}{3}}{\dfrac{2}{5}}\right)=\left[\dfrac{\dfrac{1}{3}}{\dfrac{2}{5}}\right]
$$
\left(\dfrac{\dfrac{1}{3}}{\dfrac{2}{5}}\right)=\left[\dfrac{\dfrac{1}{3}}{\dfrac{2}{5}}\right]
1 лайк
Спасибо за совет! 