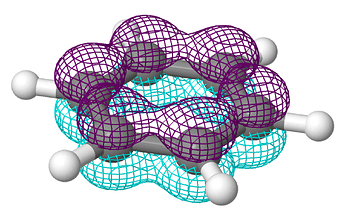
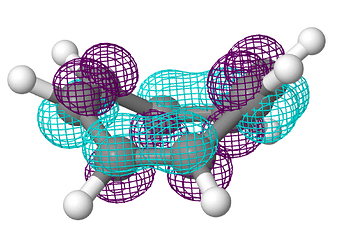
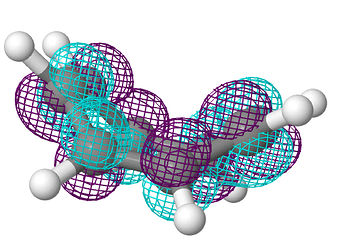
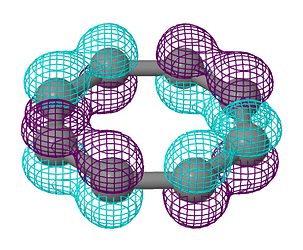
Строго говоря решений 8 (количество равное степени многочлена). Но три из решений повторяются дважды.
К слову, уравнение x^8-8x^6+20x^4-16x^2=0 довольно несложно решить аналитически, без калькулятора, просто с ручкой и листочком) Бонусные пирожки тем, кто понял как.
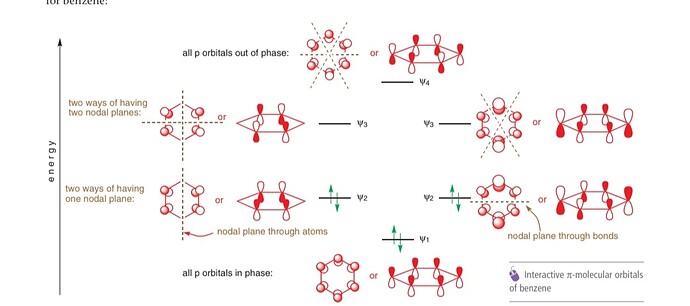
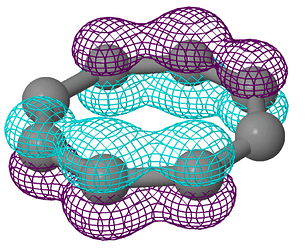
Теперь вернемся к волновым функциям. Давайте запишем волновые функции как вектора коэффициентов \left(c_1, c_2, c_3, c_4, c_5, c_6, c_7, c_8 \right), что при умножении на базис, т.е. АО углерода:
\vec{\phi} =
\begin{pmatrix}
\phi_1 \\ \phi_2 \\ \phi_3 \\ \phi_4 \\ \phi_5 \\ \phi_6 \\ \phi_7 \\ \phi_8
\end{pmatrix}
Будет давать нашу искомую МО:
\psi = c_1 \phi_1 + c_2 \phi_2 + c_3 \phi_3 + c_4 \phi_4 + c_5 \phi_5 + c_6 \phi_6 + c_7 \phi_7 + c_8 \phi_8
Так вот, коэффициенты МО (по возрастанию энергии)
\begin{align}
\Psi_1 &= \left(1, 1, 1, 1, 1, 1, 1, 1\right) \\
\Psi_2 &= \left(\sqrt{2}, 1, 0, -1, -\sqrt{2}, -1, 0, 1\right) \\
\Psi_3 &= \left(-1, -\sqrt{2}, -1, 0, 1, \sqrt{2}, 1, 0\right) \\
\Psi_4 &= \left(0, -1, 0, 1, 0, -1, 0, 1\right) \\
\Psi_5 &= \left(-1, 0, 1, 0, -1, 0, 1, 0\right) \\
\Psi_6 &= \left(-\sqrt{2}, 1, 0, -1, \sqrt{2}, -1, 0, 1\right) \\
\Psi_7 &= \left(-1, \sqrt{2}, -1, 0, 1, -\sqrt{2}, 1, 0\right) \\
\Psi_8 &= \left(-1, 1, -1, 1, -1, 1, -1, 1\right)
\end{align}