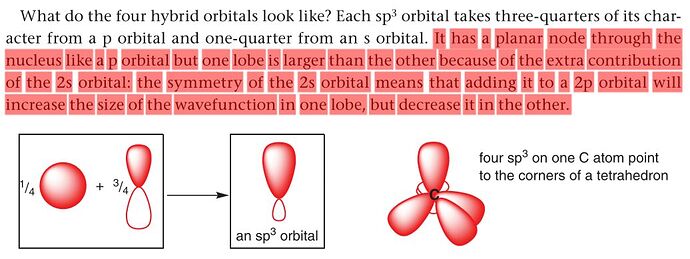
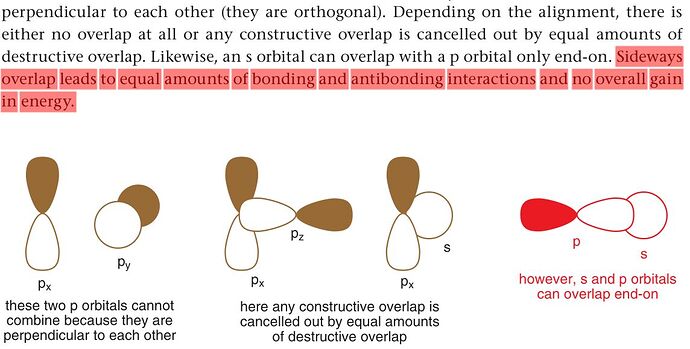
Я тут повторяя Клэйден наткнулся на одну проблему. Не понял как s орбиталь увеличивает одну часть p орбитали, уменьшая другую часть. Сперва подумал, что центр s орбитали расположен в центре p орбитали так что одна часть сферы реагирует с красной частью, а другой с белой частью. Звучало логчино. Но потом вспомнил, что до этого говорилось, что так образуется два одинаковых bonding и antibonding orbitals, которые кенцелят друг друга. Правильная версия когда происходит side-on overlap. Но в таком случае просто одна часть увеличивается и всё, то есть вторая часть будет кажатся, что она уменьшилось, а в книге говориться, что уменьшается. Клэйден стр. 98 и 100.
Это ты про взаимодействие молекулярных орбиталей на двух отдельных атомах. А тут нужно на одном и том же смотреть.
“красная” это часть p орбитали с положительной волновой функцией, а “белая” с отрицательной волновой функцией. У s орбитали только положительная волновая функция.
Если вспомнить то как накладываются волны друг на друга (интерференция волн) то красная + красная → constructive interference, а значит получится волна с большей амплитудой, а вот красная + белая → destructive interference, а значит получится волна с меньшей амплитудой.
Таким вот образом one of the lobes уменьшается, а второй увеличивается.
Отличный вопрос! Как я понял, ты как будто бы видишь противоречие из-за того, что где-то тебе говорят, что орбитали якобы не реагируют, а где-то тебе говорят, что они образуют гибридную орбиталь.
В обоих случаях мы рассматриваем линейные комбинации атомных орбиталей (АО). В случае для скриншота снизу мы смотрим на линейные комбинации двух орбиталей двух разных атомов, и пытаемся понять, будут ли эти атомы образовывать связь, используя эти АО.
Таких линейных комбинаций две, потому что изначально было две орбитали.
В случае для скриншота сверху мы смотрим на линейные комбинации четырех орбиталей одного атома и пытаемся понять, как они изменятся в случае смешивания и чем это смешивание им поможет.
Таких линейных комбинаций уже 4, потому что смешиваются 4 орбитали.
Чтобы эти орбитали образовывались, нужно понижение энергии. В случае образования связи, энергия может понижаться за счет перекрывания двух орбиталей. Если результирующий эффект (попытался перевести net effect) перекрывания орбиталей будет положительным, то энергия будет понижаться, иначе мы говорим, что орбитали не взаимодействуют друг с другом. Описать перекрывание орбиталей мы можем с помощью интеграла перекрывания — \displaystyle\int \psi_A \psi_B \text{d}\tau, где \text{d}\tau — бескончено малое приращение объема. Если брать интеграл по всему пространству, мы просуммируем все произведения \psi_A \psi_B в пространстве. Произведения будут ненулевыми только в местах перекрывания орбиталей, потому что в иных случаях значение как минимум одной из функций равно нулю. В случаях, показанных в твоем (втором) скриншоте, s орбиталь перекрывается симметрично, и с областью p орбитали, где фазы совпадают, и с областью, где фазы разные. Поэтому для каждого \psi_A(\tau_1) \cdot \psi_B(\tau_1) в области перекрывания будет противоположное по значению \psi_A(\tau_1^\prime) \cdot \psi_B(\tau_1^\prime), а значит вся сумма будет равна нулю. Поэтому стабилизации молекулы не будет, а значит и не будет взаимодействия между орбиталями (то есть не образуется связь).
В случае гибридизации, энергия понижается не за счет перекрывания орбиталей, а за счет меньшего стерического напряжения (steric strain). Почему где-то электронная плотность уменьшается, а где-то увеличивается, сказал @Galymzhan. Оно видно из того, что мы комбинируем эти функции, поэтому где-то они частично взаимоуничтожаются (destructive interference), а где-то они суммируются (constructive interference). Может еще поможет этот ответ из Chemistry StackExchange.
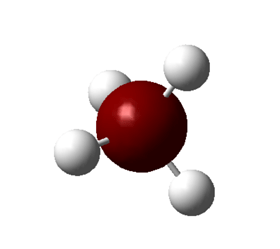
Если тебе интересно, вот так будут выглядеть линейные комбинации орбиталей в \text{sp}^3 гибридизации:
Здесь можно посмотреть на вывод коэффициентов для \text{sp}^2 гибридизации и дальше можно будет самому попытаться найти коэффициенты для \text{sp}^3 гибридизации — Thomas Engels. Quantum Chemistry and Spectroscopy. Third edition. pp. 278–281. Я обожаю эту книгу за то, что там много физики и математики. Самое интересное то, что в выводе встречаются такие интегралы, как \displaystyle\int \psi_{2s} \psi_{2p_x} \text{d}\tau и они равняются нулю ровно по той же причине, что и в случае с перекрыванием орбиталей двух разных атомов. То есть это совсем не разные вещи, как могло показаться. (По крайней я в начале думал, что это отдельные вещи.)
Если я где-то не прав или где-то есть, что дополнить, прошу поправить и дополнить.
Ты ему самое главное забыл рассказать, что метод молекулярных орбиталей(ММО) и гибридизация не женятся, т.к. это буквально разные модели строения молекул. Его заблуждение как раз в этом, он попробовал взять один метод и попробовал применить к другому.
Гибридизацию в принципе можно родить из ММО (валентные орбитали), но это такой костыль, что он почти полностью теряет свою предсказательную силу и привлекательность.
Именно так я и представляю себе гибридизацию.
Как я бы ответил на ваш вопрос? Я бы сказал так: это другое. Если мысленно представить гибридизацию как связывание s и p орбиталей – то да, у нас половина лопасти (мой перевод слова lobe) р-орбитали связывается, а другая разрыхляется. В первом приближении Хюккеля, если мы пренебрежем интегралом перекрытия S, мы получаем в общей сумме нуль: связывание и разрыхление нивелируют друг друга.
Но это не рушит картину теории гибридизации. Можно сказать, что в пустом атоме – да, действительно, орбиталям без разницы в какой форме быть. Но когда мы образуем соединение углерода с 4 атомами – гибридизованные орбитали выигрывают потому что как раз одна из их лопастей может лучше связываться с орбиталями другого атома.
Интересное примечание: если не пренебрегать интегралом S, мы получим, что гибридизованные орбитали должны быть выше по энергии, чем негибридизованные: ибо разрыхление чуть сильнее связывания. А интересно здесь то, что вроде бы это логично: мы смешиваем 2s орбитали с 2p орбиталями, а первые ниже по энергии вторых. Т.е. должно получиться что-то посередине.
Хотя, опять же, важно понимать, что теория гибридизации была придумана еще до понимания квантовой структуры атома для объяснения того почему у углерода в метане все 4 связи одинаковые если один электрон находится в s орбитали, а три в p.
И
совершенно верно. Хотя
я бы не сказал, что они прям жить друг с другом не могут. Они просто разные.
Хотя, справедливости ради, конкретно в данном случае жизнь полна иронии: гибридизацию придумали, чтобы объяснить почему все 4 связи одинаковые, и для этого родили 4 одинаковых орбитали.
А что нам скажут волновые функции метана? Давайте посмотрим (посмотрим на 5 заполненных).
n=1.
n=2
n=3
n=4
n=5
Орбитали n=3, n=4, n=5 вырожденные и сняты с одного ракурса.
Иными словами что мы имеем?) Три вырожденные орбитали и одну орбиталь пониже. Déjà vu
Как бы да, но энергия теряет для них смысл, ибо они уже не являются собственными функциями для гамильтониана. Локализованные орбитали можно родить из канонических МО (если кому-то интересно как, смотрите в книге Минкина и Симкина), но они теряют всю прелесть тогда.