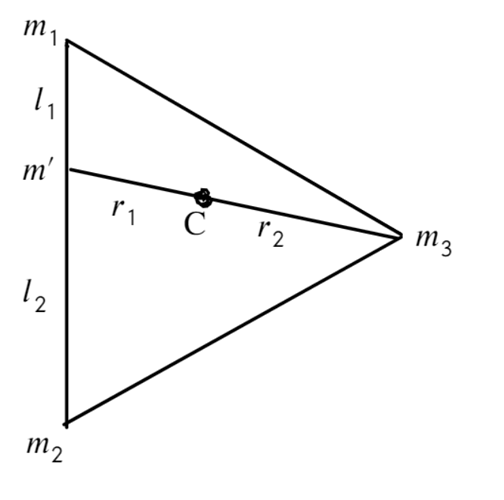
Три точечные массы m_1, m_2, m_3 связаны нитями длины l и вращаются с угловой скоростью ω вокруг центра масс, сохраняя конфигурацию равностороннего треугольника. Найдите силу натяжения всех нитей.
2 лайка
У тебя уже есть какие-то идеи, наработки решения? Или нужна подсказка к решению?
Подсказать
1 лайк
Немного теории. Если у нас есть три точки: 1, 2, 3, в таком случае центр масс можно найти двумя способами.
Решение "влоб"
Самое первое, что приходит в голову – формула нахождения центра масс
x_{cm} = \frac {\sum\limits_{i=1}^n m_ix_i} {\sum\limits_{i=1}^n m_i}\\
y_{cm} = \frac {\sum\limits_{i=1}^n m_iy_i} {\sum\limits_{i=1}^n m_i}
В данной формуле за начало координат можно брать любую точку (советую попытаться доказать это, потому что это поможет понять саму суть формулы). Простыми словами, нужно сложить произведение каждой массы на каждое расстояние и делить и всю массу системы
Другое решение
Ну вот у нас есть такой вот равносторонний треугольник
Здесь m' = m_1 + m_2. l_1 и l_2 – расстояния от точек до центра масс первой и второй масс. Они находятся очень просто через первую формулу. Будем считать, что начало системы координат – первая масса, тогда
l_1 = \frac {m_2 r}{m_1 + m_2}\\
l_2 = r \space - \space l_1 \space = \space \frac{m_1r}{m_1 + m_2}
Аналогично находим r_1 и r_2.
Далее, задача сводится к применению законов Ньютона для вращательного движения и алгебраическим выкладкам. Хочется отметить, что это нестандартная задача, в которой либо нужно очень много вычислять, либо использовать какой-то хитроумный способ, до которого я ещё не додумался
3 лайка
у меня получилась система из 12 уравнений с шестью углами в том числе)
2 лайка
Чистый гринд)
Может быть через вектора легче выйдет?
Тоже решаю эту задачу и не хватает одного шага.
Скалярно идти точно не вариант - получается огромное уравнение с шестью косинусами углов, значения у которых ужасные, и выразить оттуда силу натяжения нереально.
Векторный подход лучше: я узнал координаты векторов равнодействующих сил; каждая равнодействующая равна векторной сумме двух сил натяжения. Но в получившейся системе уравнений мне не хватает одного!
Частный случай равных масс я без проблем решил. А вот с общим засада.
Подскажите, что можно сделать.
1 лайк
По факту да, но ты свои вычисления всё равно не упростишь.
Если задать радиус-вектор из центра масс к i-й массе как \vec r_i, а силу натяжения как T_{ij}, где это натяжение стягивает i-ую массу к j-ой (понятное дело, что \vec T_{ij} = -\vec T_{ji}), то
m_i\omega^2\vec r_i = \sum_j \vec T_{ij}.
К тому же, разность попарно взятых этих радиус-векторов равняется l, или же
|\vec r_i - \vec r_j| = l.
В общем виде записанные уравнения образуют шесть уравнений с шестью неизвестными (T_1,T_2,T_3,r_1,r_2,r_3). Из первой системы уравнений
\begin{cases}
m_1\omega^2\vec r_1 = \vec T_{12} + \vec T_{13} \\
m_2\omega^2\vec r_2 = \vec T_{21}+\vec T_{23} \\
m_3\omega^2\vec r_3 = \vec T_{31} + \vec T_{32}
\end{cases}
можно взять любую пару уравнений и написать
l^2 = (\vec r_1-\vec r_2)^2 = \left(\frac{\vec T_{12} + \vec T_{13}}{m_1\omega^2} - \frac{\vec T_{21}+\vec T_{23}}{m_2\omega^2}\right)^2,
или (для определённости будем решать относительно T_{12},T_{23},T_{13})
\omega^2l^2= \left(\vec T_{12}\left(\frac{1}{m_1}+\frac{1}{m_2}\right)+\vec T_{13}\cdot\frac{1}{m_1}-\vec T_{23}\cdot\frac{1}{m_2}\right)^2.
Раскрывая квадрат и учитывая взаимное расположение векторов для скалярного произведения, получаем
\omega^2l^2 = T_{12}^2\left(\frac{1}{m_1}+\frac{1}{m_2}\right)^2 +\frac{T_{13}^2}{m_1^2} + \frac{T_{23}^2}{m_2^2} +\frac{T_{12}T_{13}}{2m_1}\left(\frac{1}{m_1}+\frac{1}{m_2}\right) +\frac{T_{12}T_{23}}{2m_2}\left(\frac{1}{m_1}+\frac{1}{m_2}\right) -\frac{T_{13}T_{23}}{2m_1m_2}.
мне уже страшно смотреть на это. Последнее уравнение можно ещё два раза получить путём взаимного обращения индексов. У кого есть желание решить полученную мной систему?)
6 лайков
Перепроверил уравнение и исправил несколько ошибок:
ω^4l^2 = T_{12}^2(\frac{1}{m_1}+\frac{1}{m_2})^2 + \frac{T_{13}^2}{m_1^2} + \frac{T_{23}^2}{m_2^2} + \frac{T_{12}T_{13}}{m_1}(\frac{1}{m_1}+\frac{1}{m_2}) +\frac{T_{12}T_{23}}{m_2}(\frac{1}{m_1}+\frac{1}{m_2}) - \frac{T_{13}T_{23}}{m_1m_2}.
Можно убедиться в его корректности, если проверить частный случай равных масс.
Но как лучше решить такую систему - пока думаю.
1 лайк
там скалярное произведение происходит, и вдобавок идёт либо \cos(\pi/3), либо \cos(2\pi/3), двойки в знаменателях при T_iT_j должны оставаться
Но там же еще двойки из удвоенных произведений. В итоге все двойки сокращаются.
а, ну тогда всё норм
Это выглядит так, будто существует какая-то приведенная масса, которая всё сделает легче и проще, или что в полярных координатах надо полностью всё записывать, или что может перейти к криволинейной системе координат, где T базисные…
1 лайк
я вообще хотел сначала изощриться и сказать, что раз уж каждое уравнение описывает поверхность второго порядка и задача сводится к нахождению точки пересечения трёх поверхностей, то каждая поверхность может описываться уравнением
X^T AX = \omega^4l^2,
где X = \begin{pmatrix}T_{12}&T_{13}&T_{23}\end{pmatrix}^T, и матрицы коэффициентов для каждого равны
A_1=\begin{pmatrix}\displaystyle\frac{1}{\mu_{12}^2}&\displaystyle\frac{1}{2m_1\mu_{12}}&\displaystyle\frac{1}{2m_2\mu_{12}}\\\displaystyle\frac{1}{2m_1\mu_{12}}&\displaystyle\frac{1}{m_1^2}&\displaystyle\frac{-1}{2m_1m_2}\\\displaystyle\frac{1}{2m_2\mu_{12}}&\displaystyle\frac{-1}{2m_1m_2}&\displaystyle\frac{1}{m_2^2}\end{pmatrix},\quad A_2 = \begin{pmatrix}\displaystyle\frac{1}{m_{1}^2}&\displaystyle\frac{1}{2m_1\mu_{13}}&\displaystyle\frac{-1}{2m_1m_{3}}\\\displaystyle\frac{1}{2m_1\mu_{13}}&\displaystyle\frac{1}{\mu_{13}^2}&\displaystyle\frac{1}{2m_1\mu_{13}}\\\displaystyle\frac{-1}{2m_1m_{3}}&\displaystyle\frac{1}{2m_1\mu_{13}}&\displaystyle\frac{1}{m_3^2}\end{pmatrix},\quad A_3 =\begin{pmatrix}\displaystyle\frac{1}{m_{2}^2}&\displaystyle\frac{-1}{2m_2m_{3}}&\displaystyle\frac{1}{2m_2\mu_{23}}\\\displaystyle\frac{-1}{2m_2m_{3}}&\displaystyle\frac{1}{m_3^2}&\displaystyle\frac{1}{2m_3\mu_{13}}\\\displaystyle\frac{1}{2m_2\mu_{23}}&\displaystyle\frac{1}{2m_3\mu_{13}}&\displaystyle\frac{1}{\mu_{23}^2}\end{pmatrix}, \quad \mu_{ij} = \left(\frac{1}{m_i}+\frac{1}{m_j}\right)^{-1}.
Однако я не знаю [сравнительно] лёгкого способа решения через матрицы в случае с нелинейными переменными второй степени. Спросил у своей учительницы математики, сказала, что подумает.
3 лайка
Надо искать собственные вектора у матрицы
О приведённой массе я тоже думал и о других системах координат (неортогональных, например). Но всё это слишком сложные абстрактные подходы для задачи из Савченко. Скорее всего, есть какой-то простой физический метод найти натяжения, но какой?..
Ребят, забудьте, эта задача в одну строчку решается.
Центробежную силу m\omega^2\vec r можно разложить на компоненты прямоугольной системы координат (банальное \vec r =x\hat x+y\hat y). Тогда если начало координат совместить с m_1, ось x направить к m_3, то можно для m_3 записать
m_3\omega^2 y_c = T_{23}\cdot\frac{\sqrt{3}}{2}, \quad y_c =\frac{m_2}{m_1+m_2+m_3}\frac{l\sqrt 3}{2}.
Отсюда моментально получаем ответ (зная, что остальные два натяжения получаются перестановкой индексов):
T_{ij}\Bigg\rvert_{i\neq j} = \frac{m_im_j}{m_1+m_2+m_3}\omega^2l.
17 лайков
Уффф мощно мощно
1 лайк
А что за знаки сверху у Х и У .Как решать с вектором, сам по себе вектор не понятная вещь. Простите но ваше решение не понял, можно подробнее пожалуйста. До этого пытался решить теоремой косинусов и найти углы но слишком долго и сложно…