ето кто сказал… Видите в чем дело, на волновых функциях нет ярлыков “я связывающая” или “я разрыхляющая” и у нас нет оператора, применение которого к волновой функции выдало бы ее характер.
Связывающая и разрыхляющая это очень условные ярлыки, которые легко определить только в самых простых системах. Когда вы смешиваете две 1s орбитали водорода, там, как бы, не так много выбора. У одной орбитали эл. плотность в пространстве между атомами увеличивается, у другой уменьшается. Одна ниже по энергии, чем АО, другая выше. Все очевидно и однозначно.
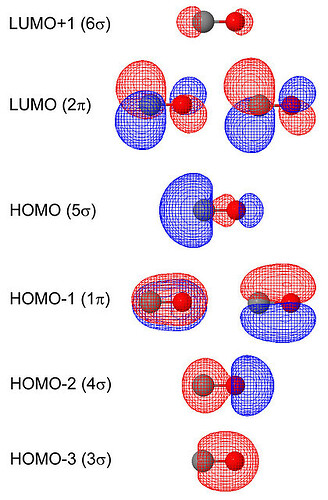
А возьмите те же МО бензола – что делает \psi_2,\psi_3 связывающими а \psi_4,\psi_5 разрыхляющими? И в первых и во вторых есть узлы, да, во вторых их больше. Но это уже не так однозначно как в случае с МО водорода, где у связывающей нет узлов, а у разрыхляющей есть.
Можно начать проводить границу по “ниже или выше энергии АО”. Но опять же это удобно работает только когда есть один тип АО с одним уровнем энергии. А что если есть разные АО? с кем сравнивать?
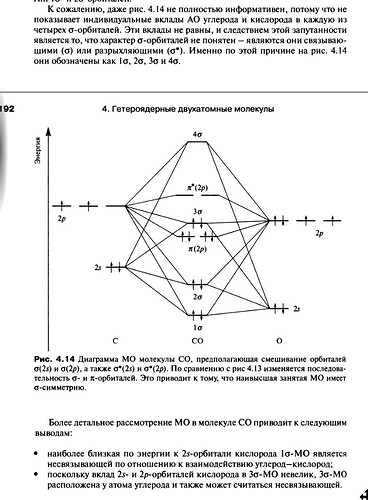
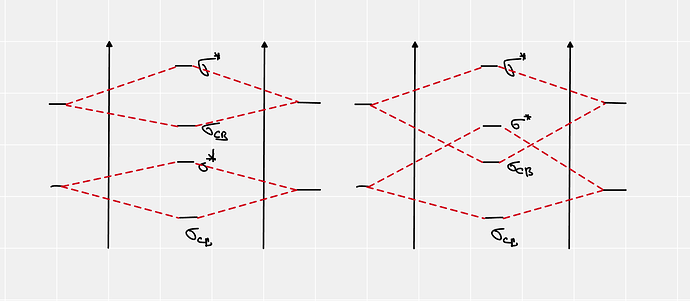
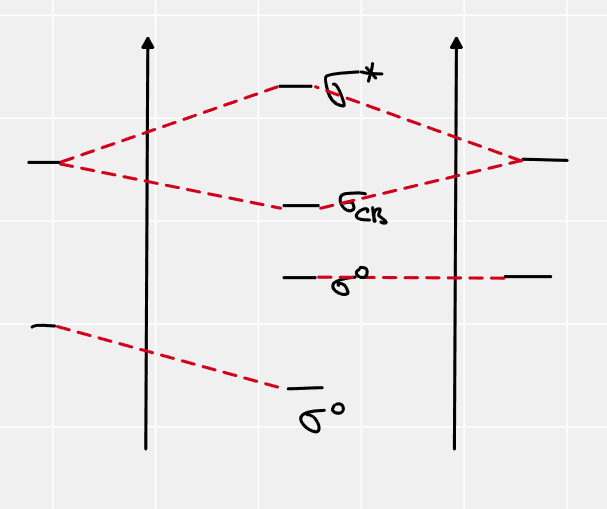
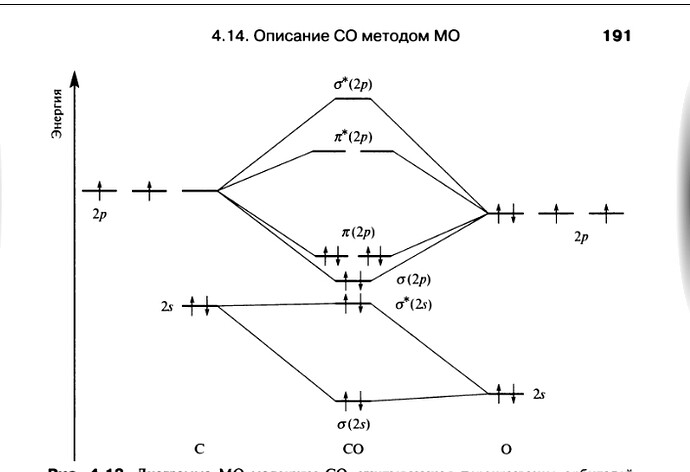
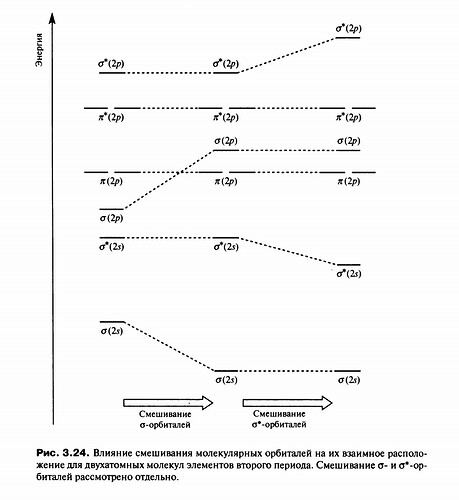
В случае СО ситуация осложняется тем, что это не типичные (ну или не примитивные) смешения двух разных АО. Чтобы построить диаграмму МО для СО надо сначала построить примитивную диаграмму, а потом добавить эффекты sp-mixing, когда часть МО реагирует с оставшимися АО. И вот там, например, одна из разрыхляющих в примитивной диаграмме орбиталей реагирует с новой АО и получает связывающий характер. Ы.
Диаграмма МО для СО на самом деле одна из самых (если не самая) сложных (нетривиальных) среди всех двухатомных молекул.
что значит упадет? от чего упадет? споткнется? не понимаю что вы пытаетесь описать. Чтобы изменилась энергия МО нужно какое-то взаимодействие с какой-то АО\МО.
да
3\sigma орбиталь без sp-mixing лежит гораздо ниже по энергии и имеет немалый вклад 2р орбиталей кислорода. Но когда включается sp-mixing c 2p углерода (он происходит, ЕМНИП, с 2\sigma и 3\sigma орбиталями, последние поднимаются по энергии ближе к 2р орбиталям углерода (и то, что они оказываются рядом с 2р кислорода это просто совпадение).