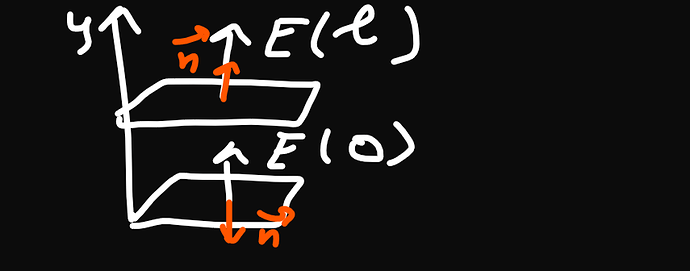У тебя уже есть какие-то идеи решения?
идеи нет
Объяснение условия
В общем, как я понял, заряды не только в кубе, а во всей области в окрестностях куба. А куб нужен лишь для задания какого-то ограниченного пространства. Тебе нужно найти заряд в этом ограниченном пространстве используя теорему Гаусса.
Подсказка 1
По теореме Гаусса
\vec E направлена вдоль оси Oy, значит поток (а \int \vec E \text d \vec S обозначает именно поток \Phi, через какую-то площадь) через грани, перпендикулярные осям Ox и Oz равны нулю
Подсказка 2
Найди разность потоков через 2 оставшиеся грани. Это и будет твой интеграл по контуру
Спасибо за подсказки! но что-то всё равно не получается
Предлагаю, тогда, рассмотреть твой ход мысли и найти момент, который всё портит (распиши свои рассуждения)
a=0\\
S = 2l^{2}\\
\frac{Q}{\epsilon_{0}} = 2El^{2}\\
E = by = bl \rightarrow Q = 2\epsilon_{0}bl^{3}
Это новый для меня раздел, поэтому заранее прошу прощения за глупую ошибку
А, всё, я понял тебя. Ты почти прав, но не совсем.
Константы
Если у тебя дана константа, которая непонятно, дана или не дана: не трогай её. От выражения a = 0, ты можешь потерять a, если она нужна, но если она сокращается, тебе от этого ни холодно, ни жарко. Просто решай с a и надейся на лучшее ![]()
Направления
Всегда следи за направлениями.
Вспомним как связано направление E и знак заряда
Если заряд положительный \Rightarrow E направлено от заряда
То же самое в теореме Гаусса. Вектор площади направлен туда, куда направлена её нормаль.
Теперь остаётся понять: куда направлен вектор нормали в теореме Гаусса?
Наружу. Чтобы понять, рассмотри точечный заряд, и к каким знакам приводят противоположные направления нормали.
Значение вектора нормали считается равным одному (он используется чисто чтобы задать направление)
Ну дальше сам попробуй
P.S.
Я и в разделах, которые годами решаю, допускаю глупые ошибки. Так что не парься, и используй ошибки, чтобы лучше понимать темы и развивать внимательность. @Alisher согласится, что внимательность, наверняка, один из самых полезных навыков в олимпиадной деятельности
я такими темпами уже афошку сливаю
А дивергенцией по объему нельзя просто? Там такая простая дивергенция просто
Дивергенцией конечно можно, только вот в самом начале изучения термодинамики такая математика еще не изучена. Кроме того, это задача из учебника, и решение предпологается через теорему Гаусса в интегральном виде.
Вы кажется \varepsilon_0 забыли, если это конечный ответ
Ах да, точно, забываю про константы постоянно. Исправил, чтобы было понятно, что я только поток посчитал.