Я понимаю, что интеграл используется когда разница бесконечно малая. Но как зависимость связано с интегралом? Можете объяснить это на примере G(энергия Гиббса)?
(dGm=Vm×dp : для тв. и жид. вещ просто (pf-pi) т.к. объем не зависит от давления; а для газа там интеграл т.к. объем газа зависит от давления)
На самом деле, и в том, и в другом случае используются интеграл, просто в первом случае он выражается через p_f - p_i, а во втором через логарифм.
В обоих случаях тебя интересует одно — какова площадь под графиком V_m-p в интервале от p_i до p_f. Поскольку вопрос в другом, не буду говорить, почему именно интересует площадь. (Но ничто не мешает задать вопрос, если этот момент неясен.)
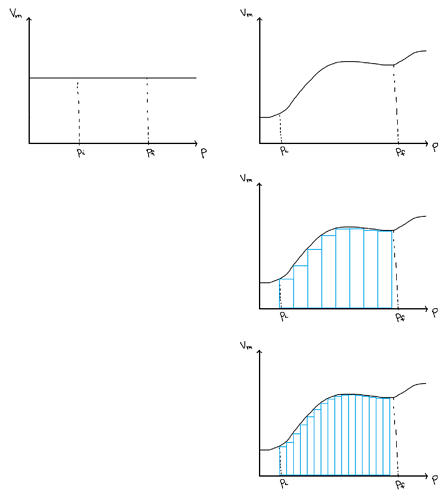
Я начеркал вот такую вот прелесть (рисунок ниже). Очень важное замечание: зависимости являются произвольными, поскольку целью было продемонстрировать саму идею интегрирования.
Мы договорились, что будем пытаться найти площадь под графиком при p \in [p_i; \ p_f]. В случае слева, значение V_m постоянно, поэтому под графиком мы получили прямоугольник. Площадь прямоугольника найти мы можем, S=V_m (p_f - p_i).
Во втором же случае под графиком получается довольно странная фигура и непонятно как вычислить ее площадь. Но мы можем сделать так: разделим отрезок [p_i; \ p_f] на несколько равных отрезков. Отметим точки, где эти отрезки заканчиваются, и проведем перпендикулярные линии так, чтобы получился прямоугольник, который лежит под графиком. Я поленился сделать расчет, поэтому у меня получилось не совсем ровно разделить отрезок [p_i; \ p_f], но получиться должно то, что изображено на рисунке в правом столбце , во второй строке. Теперь мы можем посчитать площади этих прямоугольников и суммировать их всех чтобы получить площадь под изначальным графиком.
Но справедливо будет заметить, что некоторые участки графика мы не посчитали — пустые места между прямоугольниками и самим графиком. В таком случае можно сделать следующее: уменьшим ширину каждого прямоугольника, допустим, в два раза. Тогда мы получим рисунок в правом нижнем углу. Видно, что во втором случае пустых участков, которые мы пропустили, стало меньше (по площади). То есть мы приблизились к реальному ответу. Мы можем повторить проделанное и еще раз уменьшить ширину каждого прямоугольника. Тогда мы еще ближе подберемся к реальной величине.
Уменьшая ширину прямоугольников до бесконечно малой величины \text{d}p мы сможем дойти до правильного ответа. В этом и есть суть интеграла. Для каждого прямоугольника площадь будет равна V_m(p) \cdot \text{d}p и мы все эти площади просто суммируем в каком-то промежутке, записывая это так: \displaystyle\int_{p_i}^{p_f}{V_m(p) \text{d}p}.
Чтобы понять, откуда там появился логарифм, стоит изучить математический анализ. Эта тема обсуждалась здесь — Хорошая книга по матем для химика.
Простыми словами:
Дифференцирование - это получение из простой формулы (функции) ее другую форму, которая дает мгновенную скорость по “х”. То есть находим мгновенную скорость.
Интегрирование - это из формулы, которая дает мгновенную скорость по “х”, найти изначальную простую формулу (функцию). То есть находим из скорости пройденный путь, который равен площадью под графиком.