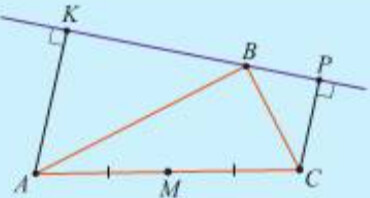
АК и СР - перпендикуляры, опущенные из вершин А и С треугольника АВС на прямую, проходящую через вершину В этого треугольника. Докажи, что середина М стороны АС равноудалена от точек К и Р.
АК и СР - перпендикуляры, опущенные из вершин А и С треугольника АВС на прямую, проходящую через вершину В этого треугольника. Докажи, что середина М стороны АС равноудалена от точек К и Р.

Давай так. Чего было бы достаточно, чтобы эти отрезки были равны? То есть, поизучай сначала чертеж того, что надо доказать.
Опустим перпендикуляр MN из M на KP.
Используя теорему Фалеса, получаем, что KN = NP. Значит, MN – и высота, и медиана в треугольнике KMP, т.е. это – равнобедренный треугольник
Можно еще так решить.
Пусть N, L середины AB и BC, соответственно.
Докажем равенство треугольников KNM и MLP.
Не сложно видеть, что \angle MNK = 90^{\circ} + \angle KNB = 90^{\circ} + \frac{1}{2} \angle KAB = 90^{\circ} + \frac{1}{2} \angle PBC = 90^{\circ} + \angle PLC = \angle PLM.
Также ML = NB = NK и MN = BL = LP.
Значит наши треугольники равны по углу и двум сторонам. Следовательно KM = MP.